伴隨函子是範疇論的基本概念之一。它在同調代數等學科中有著重要套用。
基本介紹
- 中文名:伴隨函子
- 外文名:adjoint functor
- 所屬學科:範疇論
- 別名:相伴函子
- 定義:範疇論的基本概念之一
定義
性質
簡介
等價定義
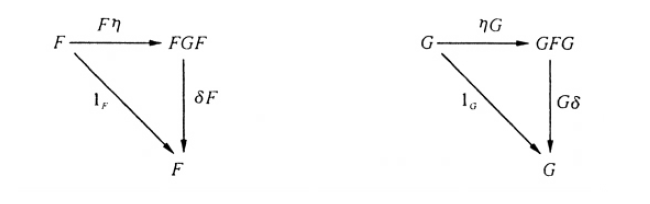

重要例子
伴隨函子是範疇論的基本概念之一。它在同調代數等學科中有著重要套用。


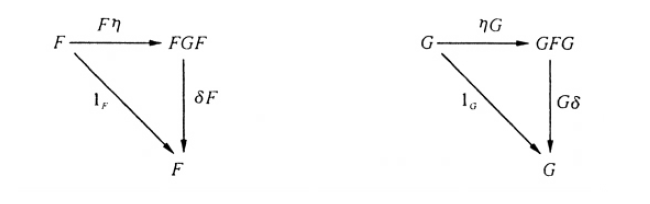



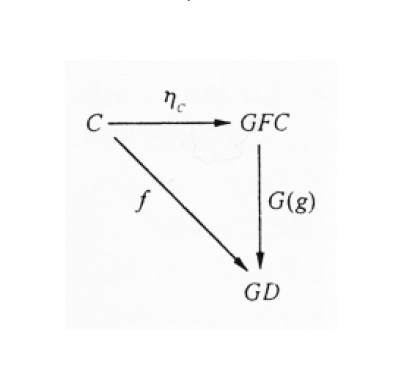
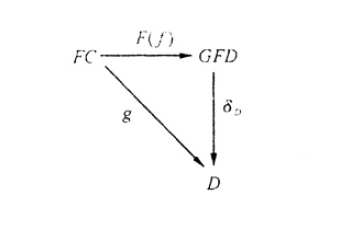
伴隨函子是範疇論的基本概念之一。它在同調代數等學科中有著重要套用。定義設A與X為範疇。從X到A的伴隨對為三元組<F,G,φ>:X→A。其中F:X→A與G:A→X為函子,函式φ在給定X中對象x與A中對象a後給出...
極限函子:對一固定的指標範疇,若每個函子 都有個極限(即若 為完全的),則極限函子 即為將每個函子映射至其極限的函子。此類函子的存在性可以由將其理解為對角函子的右伴隨函子,且引入福端伴隨函子定理來證明之。這需要一個...
無界運算元的伴隨 許多重要的運算元不是連續的或只定義在希爾伯特的一個子空間上。在這種情形,我們仍然能定義伴隨,在自伴運算元一文有解釋。其他伴隨 範疇論中,方程 形式上類似地定義了伴隨函子偶性質,這也是伴隨函子得名之由來。參見 數...
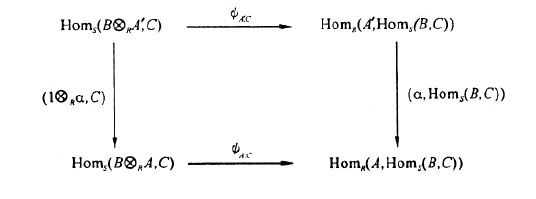
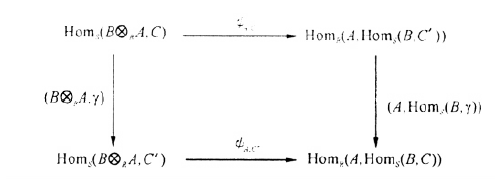
伴隨性質 Hom函子是張量函子的右伴隨。具體來說,對任何右R模A,Hom函子 右伴隨於張量函子 ;對任何左R模B,Hom函子 右伴隨於張量函子 。作為右伴隨函子,Hom函子為左正合函子,保持投射極限、積、核。
函子無論對哪個變數都是左正合的,這是左正合函子的基本例子。設 是一對伴隨函子。若 存在任意有限歸納極限,則 右正合;若存在任意有限射影極限,左正合。此法可建立許多函子的正合性。設 為拓撲空間,阿貝爾群數學範疇上的整體...
4.限制函子g : R-gr--> Re-mod , M-> M&,其中gEG,M=①,,ECM,,ER-gr,<是共變的正合函子.這些函子有以下性質:1.函子Ind和coind分別是函子的左和右伴隨函子.2.函子, ; R-gr->Re-mod是範疇等價,若且唯若...
表示函子自然同構於Hom函子,因而享有許多後者的性質。尤其值得注意的是,(協變)表示函子保持所有極限。由此可得,未能保持某些極限的函子都不是可表的。相似地,反變可表函子把余極限映到極限。3.左伴隨 如果函子 帶有左伴隨 ...
內容包括模論中的幾條基本定理和幾類特殊的模;Abel疇與正合函子,同調代數基本定理,導出函子,Ext函子和Yoneda擴張;拉回與推出,伴隨對,函子的極限理論,伴隨函子定理,Grothendieck範疇等。該書力求簡明扼要,推導充分,既充分使用...
1.2 函子 1.3 自然變換 1.4泛態射與極限 1.5伴隨函子 2 Petri網簡介 3 人工神經網簡介 3.1 概述 3.2 人工神經元模型 3.3 人工神經網路的互連結構 3.4 人工神經網路的學習 3.5 人工神經網路的套用 4 貝葉斯網簡介 4....
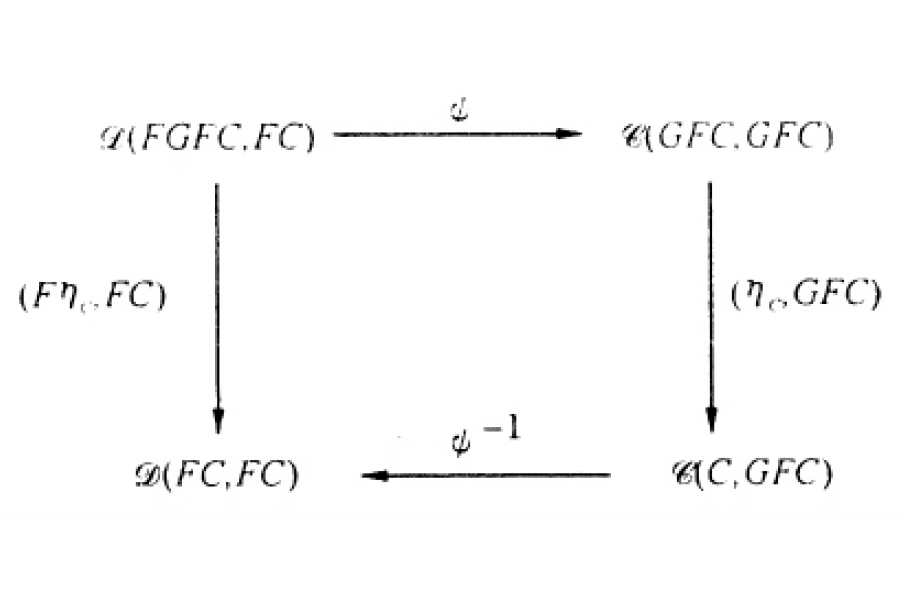
它與伴隨函子概念也有緊密聯繫。如下論斷對函子F:C→D與G:D→C等價:存在從FG到I與從I到GF的自然同構,分別叫做余單位與單位。F是G的一個左伴隨且兩個函子都完全且忠實。F是G的一個右伴隨且兩個函子都完全且忠實。從而我們...
初始和終端對象也可以根據通用屬性和伴隨函子來表征。令1是具有單個對象的離散類別(由...表示),並且令U:C→1是唯一(常數)函子為1.然後 C中的初始對象I是從·到U的普遍態射。傳送給我的函子與U相連。C中的終端對象T是從U...
語法上,上/下術語是指功能套用出現相對於≤的位置術語“伴隨”是指單調伽羅瓦對應是類別理論中的一對伴隨函子的特殊情況,如下文進一步討論的。 這裡遇到的其他術語對於較低(分別上)的伴隨是左鄰近(分別右伴)。伽羅瓦對應的基本屬性...
2.2 函子與自然變換 2.3 函子範疇 2.4 泛性質 2.5 可表函子 2.6 伴隨函子 2.7 極限 2.8 完備性 習題 第三章 么半範疇 3.1 基本定義 3.2 嚴格性與融貫定理 3.3 辮結構 3.4 充實範疇 3.5 2-範疇...
泛包絡代數函子U為李代數函子L的左伴隨函子。泛性質 以下固定域 。首先注意到:對任意帶乘法單位元的 -結合代數 ,定義括積 ,可視 為李代數。泛包絡代數系指帶單位元的結合代數 及一個指定的李代數同態 。這對資料由...
反過來說,通過序理論的伴隨函子定理,保持所有上確界/下確界的映射只要滿足額外的條件就可以被當作伽羅瓦連線的一部分。分配律 格L是分配格,如果對於所有L中的x,y和z,滿足 但是這只是聲稱了交函式∧:L->L保持二元上確界。在格...
N a generalization in category theory of this notion 伴隨矩陣 短語搭配 adjoint process[數] 伴隨過程 adjoint flux[核] 伴隨中子通量 ; 伴隨通量 ; 伴隨中子通量 adjoint graph 導出圖 ; 詳細翻譯 adjoint functor[數] 伴隨函子 ...
對範疇的系統研究起始於S.Eilenberg和S.MacLane在代數拓撲學中的工作,他們在1945年提出範疇、函子和自然變換等基本概念,其後,在1958年,D.Ken明確地定義並研究了伴隨函子和一般極限理論,在20世紀60、70年代,F.w.Iawvere將範疇...
即他們滿足:在通用邏輯中,閉包運算元也被稱為結果運算元。在理論計算機科學中重要的部分有序集理論中,閉包運算元有另外的定義。推廣 如上面提及的,閉包可以被看作來自伽羅瓦連線。如果把伽羅瓦連線推廣為伴隨函子,閉包的對應是monad。
13.5 導出函子 13.6 群同調 13.7 非交換上同調群 習題 第十四章 範疇 14.1 函子 14.2 例子:箭圖表示 14.3 可表函子 14.4 伴隨函子 14.5 極限 14.6 纖維範疇 14.7 Abel範疇 14.8 三角形 14.9 復形 習題 索 ...
4.1 伴隨函子 42 4.2 偏Doi-Hopf群模範疇的可分函子 45 4.3 套用 51 第5章 廣義偏扭曲Smash積的性質與Morita關係 55 5.1 廣義偏Smash積 55 5.2 廣義偏扭曲Smash積 58 5.3 Morita關係 62 第6章 偏扭曲Smash積 68 6...
該範疇是Cartesian閉的若且唯若三角模是冪等的. 最後, 在模糊拓撲理論方面, 利用強化範疇中的基底變換方法, 構造了分明集合上的模糊拓撲範疇和模糊集合上的模糊拓撲範疇之間的一對伴隨函子, 使得前者可以作為余反射的滿子範疇嵌入到後者...
第5章伴隨115 51Galois對應115 VIII高級範疇論 52泛映射117 53餘泛映射125 54伴隨與伴隨函子130 55伴隨的存在性139 56伴隨與極限140 第6章計算機科學中的範疇145 61函式式程式設計語言構成的範疇145 62演繹系統構成的範疇146 63帶...
本身也會是個範疇。其中存在一自然函子 ,稱之為包含函子,單純為物件和態射的恆等函式。一個範疇 的完全子範疇是一個 的子範疇 ,會使得每對在 內的物件 和 , 一個完全子範疇是一個包括著在 的物件間“所有”態射...
