基本介紹
- 中文名:伯格曼空間
- 外文名:Bergman space
- 領域:數學
- 性質:解析函式空間
- 提出者:伯格曼
概念
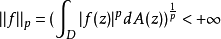

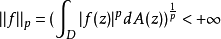

伯格曼空間(Bergman space)是區域上平方可積的解析函式空間。數學中,函式空間指的是從集合 X 到集合 Y 的給定種類的函式的集合。其叫做空間的原因是在很多套用中...
伯格曼投影是希爾伯特空間L2(D)到伯格曼空間的正交投影運算元,P稱為伯格曼投影。...... 表示了希爾伯特空間L2(D)到伯格曼空間的正交投影運算元,P稱為伯格曼投影,其中K(z...
伯格曼核函式是刻畫有界域函式論性質和幾何性質的一個極有用的正值函式。...... 伯格曼核函式是刻畫有界域函式論性質和...,記μ為Cn的歐幾里得測度,考慮函式空間...
伯格曼度量(Bergman metric)由伯格曼核函式誘導的克勒度量。伯格曼核函式和伯格曼度量是研究有界域的幾何性質及函式論性質的基本工具之一。克勒度量是特殊的埃爾米特...
布洛赫空間(Bloch space)一類重要的解析函式空間。解析函式是指能局部展成冪級數的函式,它是複變函數論研究的主要對象。解析函式類包括了數學及其在自然科學和技術...
英格瑪·伯格曼(Ernst Ingmar Bergman),1918年7月14日出生於瑞典烏普薩拉,瑞典導演、編劇、製作人。1944年,編寫個人第一個電影劇本《苦悶》。1946年,執導個人第一部...
《伯格曼》是由荷蘭Graniet Film BV、Epidemic聯合製作的113分鐘驚悚影片。該片由亞歷斯·馮·華麥丹編劇、執導並主演,揚·貝弗特、哈德薇奇·米尼斯、傑洛恩·...
瑞典導演、劇作家和影片製作人。生於烏普薩拉市,父親是牧師。伯格曼從學生時代開始參加學生劇團演出,擔任過業餘話劇團團長。1940~1942年任斯德哥爾摩歌劇院助理導演。...
《伯格曼經典作品集(DVD)》是峨眉電影製片廠音像出版社2005年出版的圖書,由英格瑪·伯格曼編著。...
由瑞典著名導演英格瑪·伯格曼於1949年執導拍攝的劇情片。影片主要講述了作家與其妻子、情人之間的糾葛,展現了一群無法得到愛的芸芸眾生。電影很好的體現了導演對劇本...
《假面》是由英格瑪·伯格曼執導,畢比·安德森、麗芙·烏曼主演的懸疑電影,於1966年10月18日在瑞典上映。該片講述了護士阿爾瑪在與女演員伊莉莎白相處的過程中漸漸...
