事件代數(event algebra)是一種特殊的布爾代數,設P(Ω)是適合某種條件的所有事件的全體,Ω與∅分別是必然事件與不可能事件,∪,∩,-分別是事件的和、積、逆運算,則布爾代數〈P(Ω),∪,∩,-,Ω,∅〉稱為事件代數。
基本介紹
- 中文名:事件代數
- 外文名:event algebra
- 所屬學科:數學(布爾代數)
- 簡介:布爾代數的推廣
基本介紹













相關說明












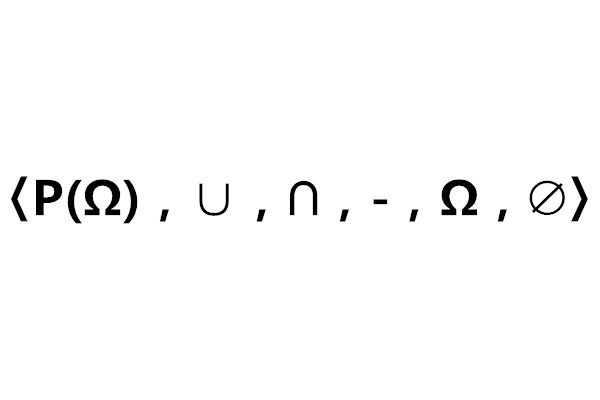
事件代數(event algebra)是一種特殊的布爾代數,設P(Ω)是適合某種條件的所有事件的全體,Ω與∅分別是必然事件與不可能事件,∪,∩,-分別是事件的和、積、逆運算,則布爾代數〈P(Ω),∪,∩,-,Ω,∅〉稱為事件代數。

























事件代數(event algebra)是一種特殊的布爾代數,設P(Ω)是適合某種條件的所有事件的全體,Ω與∅分別是必然事件與不可能事件,∪,∩,-分別是事件的和、積、逆運算,則布爾代數〈P(Ω),∪,∩,-,Ω,∅〉稱為...
條件/事件系統(condition/event system)是2018年全國科學技術名詞審定委員會公布的計算機科學技術名詞,出自《計算機科學技術名詞 》第三版。定義 設Σ=(B,E;F,)為一個基本網系統,C是Σ的完全情態集。若(B,E;F)是一個簡單網,...
代數(algebra),是由算術(arithmetic)演變來的,這是毫無疑問的。至於什麼年代產生的代數學這門學科,就很不容易說清楚了。比如,如果你認為“代數學”是指解bx+k=0這類用符號表示的代數方程的技巧。這種“代數學”是在十六世紀才...
是模糊事件A的機率(probability of a event A),稱為模糊 -代數 上的模糊機率測度(Fuzzy probability measure),稱 為 生成的模糊機率空間,即模糊事件的機率測度空間。的下標Z表示 是Zadeh意義下的模糊機率測度。如果 是可測集,...
在機率空間的度量理論定義下,不需要定義基本事件的機率。特別地,定義機率的事件集合可以是S上的一些σ代數,而不一定是全集。特點 在機率計算中,每一種可能的出現情況稱為一個“基本事件”。基本事件必須具有以下特點:(1)任何兩個...
極小極大代數 algebra一種特殊的雙子代數,記為 一(M,①,⑧) 中文名 極小極大代數 外文名 algebra 極小極大代數 algebra一種特殊的雙子代數,記為 l一(M,①,⑧),其中M=Y`n;EZ, t;EZ,Z=ZU{一二},Z =ZU{+二}.“加法”...
則稱 F 為波雷爾(Borel事件域),或 事件域或 代數。波雷爾事件域中每一個樣本空間的子集稱為一個事件。( Ω,F )為可測空間。基本類型 1.樣本空間包含可列(可數)的元素,從而事件域包含可列個事件,生成的機率是離散...
本項目詳細地分析了現有的相關研究,針對事件本體形式化中的若干關鍵技術提出了自己的研究思路,取得了一系列的研究成果,主要包括:(1)提出基於框架的概念代數的事件和事件類表示方法,同時對事件的對象、環境、時間、動作等要素進行了基於...
群論之後,多種代數系統(環、域、格、布爾代數、線性空間等)被建立。這時,代數學的研究對象擴大為向量、矩陣,等等,並漸漸轉向代數系統結構本身的研究。上述兩大事件和它們引起的發展,被稱為幾何學的解放和代數學的解放。19世紀還...
《工程數學---線性代數與機率統計》是2018年1月清華大學出版社出版的圖書,作者是呂隴、姚小娟、李建生、郭中凱、任秋艷、楊宏。內容簡介 《工程數學——線性代數與機率統計》是在高等教育大眾化和辦學層次多樣化的新形勢下,結合工科學生...
對於事件元的選擇體現了命運的複雜性。影響和制約一個人命運的因素(FACTORS)非常複雜,將這些因素進行權重分配,事實上,它們所發生作用並非以簡單的代數級運算為標準,研究引發事件元變化的各個因素,可以獲得諸多因素與事件元的選擇成模糊...
進程代數是關於通信並發系統的代數理論的統稱。 20世紀70年代後期,英國學者RMnner和C. A.R,分別提出了通信系統演算和通信順序進程,開創了用代數方法研究通信並發系統的先河。 此後這一研究方向興盛不衰,出現了眾多類似而又 相互區別的...
本書是針對獨產學院開設公共基礎課大學數學而編寫的,涵蓋了線性代數和機率統計的基礎知識,內容包括行列式、矩陣、線性方程組、矩陣特徵值、事件與機率、隨機變數、大數定律、統計等基本知識,同時配備了適當難度的教學例題和習題。本書編寫...
旨在為描述高階模糊邏輯中模糊事件的可能性奠定代數基礎,同時為剩餘格、超EQ-代數和相等代數上態的研究提供新的思路和方法。結題摘要 非經典邏輯代數是不確定性數學理論的重要研究領域,EQ-代數是高階模糊邏輯對應的一類重要的邏輯代數。
1.1.1 隨機現象、隨機試驗和隨機事件 1.1.2 事件σ-代數 1.1.3 機率的公理化定義,機率空間 1.1.4 機率的基本性質 1.1.5 條件機率和事件的獨立性 1.2 隨機變數及其分布 1.2.1 隨機變數的數學定義 1.2.2 隨機變數的...
( 5)運用布爾代數規則簡化事故樹 , 即整理出頂上事件與若干最小割集 ( x 1 , x 2 , x 3 …x n)之間的關係 ,然後按一定的規則算出各基本事件對頂上事件的影響力度的相對結構重要度係數 , 從而對各基本事件的結構重要度排序...
(1)確定事件間的關係,進行事件的運算;(2)利用事件的關係進行機率計算;(3)利用機率的性質證明機率等式或計算機率;(4)有關古典概型、幾何概型的機率計算;(5)利用加法公式、條件機率公式、乘法公式、全機率公式和貝葉斯公式計算機率...
這個小馬爾科夫(1903-1979)的名字及父名與父親完全相同,後來也成了著名的數學家,先研究理論物理和天體力學,後轉向動力體系理論、測度論、拓樸學、代數等,並於1953年當選為蘇聯科學院通訊院士。1918年秋,馬爾科夫因患青光眼回到彼得堡...
獨立在數學中套用廣泛,包括線性代數中的向量獨立、機率論中的獨立、公理系統的獨立等。線性代數中的向量獨立 線性代數中的向量獨立(線性無關),即兩個向量不成比例,不可互相表示,沒有多餘。聯繫:生活中的獨立,獨立的人,即人的...
▪ 計算機時代 ▪ 計算歷史 ▪ 算準記錄 2 記號 3 公式 4 特性 ▪ 幾何 ▪ 代數 ▪ 數學分析 ▪ 數論 ▪ 機率論 ▪ 統計學 ▪ 物理學 5 國際圓周率日 6 趣聞事件 圓周率...
某個事件E的機率P(E)是定義在“全體”(universe)或者所有可能基礎事件的樣本空間Omega時,機率P必須滿足以下柯爾莫果洛夫公理。 也可以說,機率可以被解釋為定義在樣本空間的子集的西格馬代數(\sigma-Algebra)上的一個測度,那些子集為...
1984年S.Brooks,托尼·霍爾和W.Roscoe提出CSP理論(TCSP)。這是一個代數演算系統,其基本成分是事件(或動 作)。進程由事件和一組運算元構造而成。典型的運算元有:→(前綴),|(外部非確定性選擇),\e(事件隱蔽),以及遞歸等。例子 ...
