二元布爾代數(binary Boolean algebra)亦稱簡單布爾代數，是一種常用的布爾代數，指論域僅含兩個相異元素的布爾代數。
基本介紹
- 中文名：二元布爾代數
- 外文名：binary Boolean algebra
- 所屬學科：數學（形式邏輯）
- 別稱：簡單布爾代數
- 特點：論域僅含兩個相異元素
二元布爾代數的特點,二元布爾代數上的布爾函式,
二元布爾代數的特點
二元布爾代數的特點是：
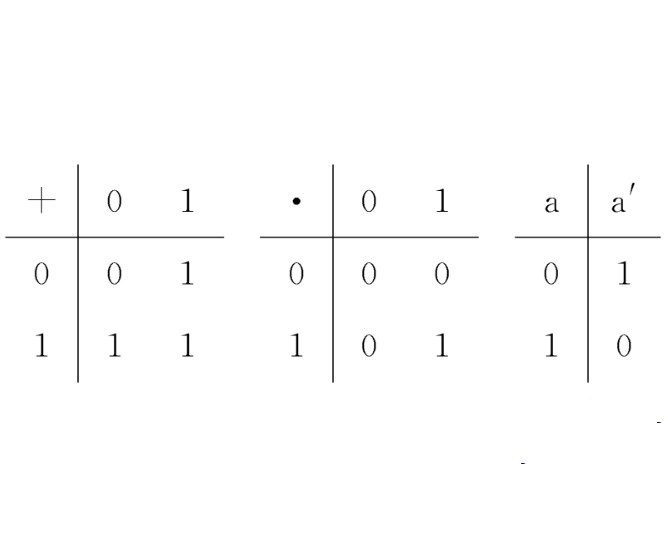
1.B={0，1}，且其運算可用下面諸表列出：
+ | 0 | 1 |
0 | 0 | 1 |
1 | 1 | 1 |
· | 0 | 1 |
0 | 0 | 0 |
1 | 0 | 1 |
a | a' |
0 | 1 |
1 | 0 |
2.二元布爾代數可用{0}是它的惟一的真理想來刻畫，即在布爾代數B中，B={0，1}若且唯若{0}是B的惟一的真理想。
3.B的哈塞圖如下圖所示。
4.若0和1分別表示真值假和真，則在{0，1}上的布爾運算+，·，′分別表示三種邏輯運算：析取、合取和否定。
5.可以證明任何二元布爾代數都是同構的。
二元布爾代數上的布爾函式
定理：二元布爾代數
上的一個任意n元函式，都是布爾函式。
下面我們給出確定這個函式的布爾表達式的兩種方法。
1．主析取範式
幾個變元
的一個布爾表達式，如果它有形式：
在
上的一個布爾表達式，如果它是一些小項的並，則稱它為主析取範式。
具體地說，對於函式值為1的有序的0和1的n元組，有一個小項：
2．主合取範式
n個變元的一個布爾表達式，如果它有形式：
在上的一個布爾表達式，如果它是大項的交，則稱它為主合取範式。
具體地說，對於函式值為0的有序的0和1的n元組，有一個大項：
