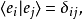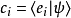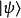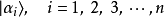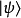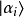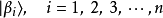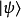不相容可觀察量

在物理學里，特別是在量子力學里，處於某種狀態的物理系統，它所具有的一些性質，可以經過一序列的物理運作過程而得知。這些可以得知的性質，稱為可觀察量（observable）。假若兩種可觀察量的對易算符不等於0，則稱這兩種可觀察量為“不相容可觀察量”。

基本介紹

• 中文名：不相容可觀察量
• 外文名：Incompatibility of observables in quantum mechanics
• 領域：量子力學
• 對易算符：不等於0

可觀察量

在物理學里，特別是在量子力學里，處於某種狀態的物理系統，它所具有的一些性質，可以經過一序列的物理運作過程而得知。這些可以得知的性質，稱為可觀察量（observable）。例如，物理運作可能涉及到施加電磁場於物理系統，然後使用實驗儀器測量某物理量的數值。在經典力學的系統里，任何可以用實驗測量獲得的可觀察量，都可以用定義於物理系統狀態的實函式來表示。在量子力學裡，物理系統的狀態稱為量子態，其與可觀察量的關係更加微妙，必須使用線性代數來解釋。根據量子力學的數學表述，量子態可以用存在於希爾伯特空間的態矢量來代表，量子態的可觀察量可以用厄米算符來代表。

數學表述

本徵態

假設，物理量O是某量子系統的可觀察量，其對應的量子算符 ，可能有很多不同的本徵值 與對應的本徵態 ，這些本徵態 ，形成了具有正交歸一性的基底：

其中， 是克羅內克函式。

任何描述這量子系統的量子態 ，都可以用這基底的本徵態表示為

其中， 是復係數，是在量子態 里找到量子態 的機率幅。

假設，量子態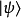 等於這些本徵態之中的一個本徵態 ，則對於這量子系統，測量可觀察量O，得到的結果必定等與本徵值 ，機率為1，量子態 是“確定態”。

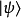
統計詮釋

根據統計詮釋，對應於可觀察量的量子算符可能有很多本徵值，測量結果只能是其中一個本徵值，而且，每一個本徵值出現的機會呈機率性。測量這個動作會將量子系統的量子態改變為對應於本徵值的本徵態，並且，在之後短暫片刻內，量子系統的量子態仍舊是這本徵態。

假設，某量子系統的量子態為

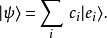
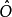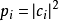測量這個動作會將量子系統的量子態改變為算符 的一個本徵態。假設量子態改變為本徵態 ，則改變為這本徵態的機率為 ，測量結果是本徵值 ，得到這本徵值的機率也為 。在測量之後短暫片刻內，量子系統的量子態仍舊是本徵態 。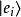

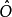
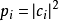
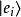
將算符 作用於量子態 ，會形成新量子態 ：

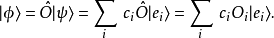
從左邊乘以量子態 ，經過一番運算，可以得到

所以，每一個本徵值與其機率的乘積，所有乘積的代數和就是可觀察量O的期望值：

厄米算符

每一種經過測量而得到的物理量都是實數，因此，可觀察量O的期望值是實數：

對於任意量子態 ，這關係都成立：

根據伴隨算符的定義，假設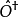 是 的伴隨算符，則 。因此，

這正是厄米算符的定義。所以，表現可觀察量的算符，都是厄米算符。

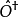
不相容可觀察量

假若兩種可觀察量的對易算符不等於0，則稱這兩種可觀察量為“不相容可觀察量”：

其中， 、 分別是可觀察量A、B的算符。

這兩種算符 與 絕對不會有共同的基底。一般而言， 的本徵態與 的本徵態不同假設量子系統的量子態為 。對於算符 ，所有本徵值為 的本徵態 ，形成一個基底。量子態 可以表示為這組基底本徵態的線性組合：

其中， 是復係數，是在量子態 里找到量子態 的機率幅。

對於算符 ，所有本徵值為 的本徵態 ，形成了另外一個基底。量子態 可以表示為這組基底本徵態的線性組合：

其中， 是復係數，是在量子態 里找到量子態 的機率幅。

對於量子系統的可觀察量A做測量，可能得到的結果是各種本徵態 的本徵值 ，獲得這些不同結果的機會具有機率性，可以表達為機率分布，結果為 的機率是 。

假設測量的結果是本徵值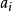 ，則可以推斷，在測量之後短暫片刻內，量子態是本徵態 。假若立刻再測量可觀察量A，由於量子態仍舊是本徵態 ，所得到的測量值是本徵值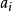 機率為1。假若立刻再對本徵態 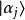測量可觀察量B，則會得到統計性的答案。假設測量的結果是本徵值 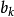，則可以推斷，在測量之後短暫片刻內，量子態是本徵態 。

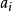
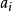
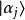
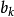
根據不確定性原理，

設定 。假設，A與B是兩個不相容可觀察量，則 。而A的不確定性與B的不確定性的乘積 ，必定大於或等於 。

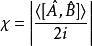
實例

為了具體計算位置與動量的期望值，可以將量子態表現於位置空間，以位置空間的波函式來表示，使用對應的代數算符。

位置與動量

位置x，動量p都是可觀察量，它們的算符都是厄米算符：

角動量

在三維空間裡，角動量算符的x-分量 是厄米算符。因為

其中，y與z分別是位置的y-分量與z-分量， 與 分別是動量的y-分量與z-分量。

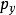
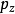
類似地，角動量算符的y-分量 也是厄米算符。

參閱

• 位置算符
  
• 動量算符
  
• 角動量算符
  
• 哈密頓算符