基本介紹
- 中文名:動量算符
- 外文名:momentum operator
- 學科:量子力學
- 對象:微觀粒子
- 本徵態:平面波
- 本徵值分類:取離散譜或連續譜
定義介紹
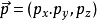
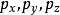
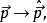
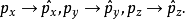
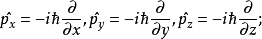
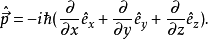
本徵方程
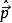
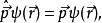
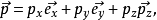
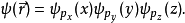

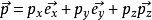
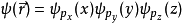
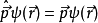
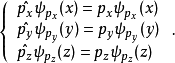
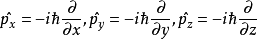
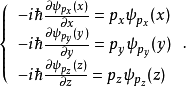
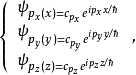
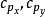
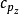
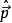
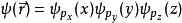
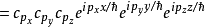
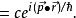
波函式
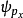
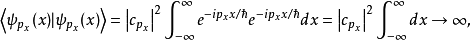
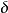
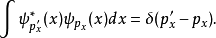
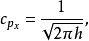
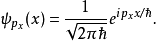
對易式
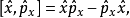
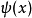
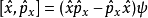
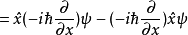
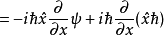
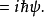
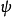
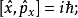
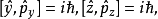
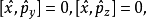
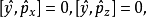
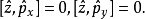
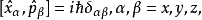
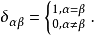
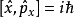
物理意義
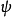
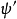
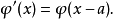
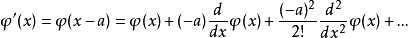
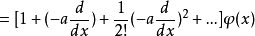
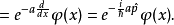
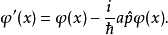
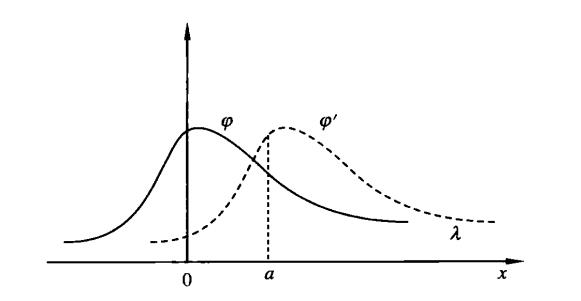 狀態平移
狀態平移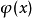
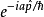
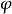
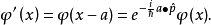
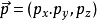
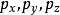
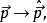
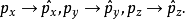
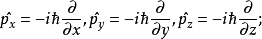
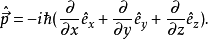
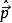
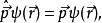
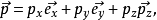
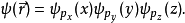

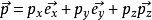
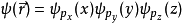
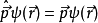
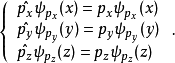
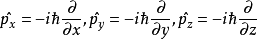
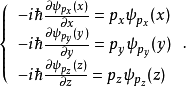
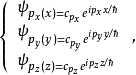
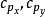
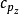
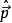
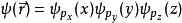
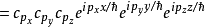
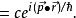
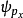
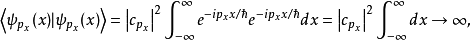
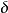
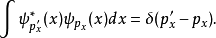
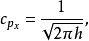
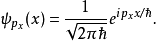
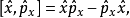
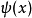
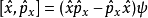
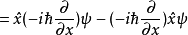
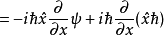
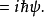
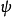
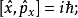
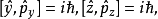
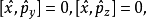
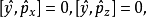
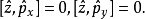
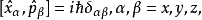
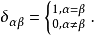
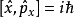
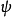
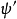
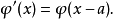
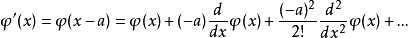
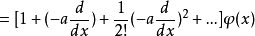
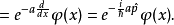
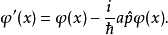
 狀態平移
狀態平移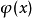
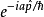
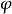
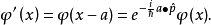
動量算符是在量子力學中表示微觀粒子的動量的算符。動量算符是表示力學量的厄米算符。...
動量表象指選取代表動量空間的完備基矢(動量算符的本徵矢),來描述物理態對應的矢量、可觀測量對應的算符以及物理學規律所對應的方程的一種表示方法。...
使問題從一種狀態變化為另一種狀態的手段稱為操作符或算符。算符在單獨存在時是沒有什麼意義。操作符可為走步、過程、規則、數學運算元、運算符號或邏輯符號等。....
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。即厄米算符表達了一...
量子力學中的力學量和算符基本信息 編輯 在量子力學中,當微觀粒子處於某一狀態時,它的力學量(如坐標、動量、角動量、能量等)一般不具有確定的數值,而是具有一...
這個方程在這個形式下充分顯示出了時間與空間的對應性(時間與能量相對應,正如空間與動量相對應,後述)。這種算符(物理量)不隨時間變化而狀態隨時間變化的對自然...
算符表示力學量的算符,在不同表象中也有不同的表示形式。在坐標表象中, 各種力學量的算符形式是 6 是動量算符。算符7 作用在波函式ψ(x,t)上得到另一...
哈密頓量是一個物理辭彙,是系統的能量算符,是一個描述系統總能量的算符,以H表示。哈密頓量在大部分的量子理論公式中十分重要。...
在量子力學裡,埃倫費斯特定理(Ehrenfest theorem)表明,量子算符的期望值對於時間的導數,跟這量子算符與哈密頓算符的對易算符相關。...
對易的算法,即算符的對易關係(Commutation relation)。設F和G為兩個算符,若FG-GF=0,則F和G對易;若FG-GF≠0,則F和G不對易。...
在這樣的定義下,兩個角動量算符的的耦合表達為:容易驗證這樣定義的j滿足角動量的基本對易關係,因此是一個角動量算符,稱為總角動量算符。...
但對於非笛卡爾坐標,如平面極坐標和球面坐標系,動量算符的整體形式及各方向分量形式卻很容易讓人產生誤解,這在一般的量子力學教材中幾乎沒有提及。尹世忠給出了球...
1.3.1 角動量算符的基本性質1.3.2 兩個角動量的耦合1.3.3 3個角動量的耦合1.3.4 4個角動量的耦合1.4 不可約張量及其角向矩陣元...
為動量算符(p= −iħ∇,∇為梯度算符),為泡利矩陣,為泡利旋量。兩個旋量分量都滿足薛丁格方程這表示系統是有額外但簡併的的自由度。另可看出泡利方程...
在量子力學中,可觀測的力學量A以算符的形式出現,代表對波函式的一種運算。例如,在坐標表象下,動量算符對應的A稱為力學量的本徵值,ψ稱為力學量的本徵態。...
對於像質子、中子及原子核這樣的亞原子粒子,自旋通常是指總的角動量,即亞原子...對角動量算符的討論——對自旋的討論之三[J]. 大學物理, 2001, 20(1): ...
將動量算符代入式子中,從而得到狄拉克方程:亦可以矢量符號寫為:其中的係數 和 不能是簡單的常數,否則即使對於簡單的空間旋轉變換,這個方程也不是洛倫茲協變的。...
角動量算符及其一般理論 參考資料 1. Rasch, J.; Yu, A. C. H. Efficient Storage Scheme for Pre-calculated Wigner 3j, 6j and Gaunt Coefficients. ...
第20章 算符 §20-1 操作與算符 §20-2 平均台皂量 §20-3 原子的平均能量 §20-4 位置算符 §20-5 動量算符 §20-6 角動量 §20-7 平均值隨時...
1.2 算符與力學量51.2.1 算符51.2.2 力學量的表示71.2.3 力學量的取值81.3 電子在庫侖場中的運動101.3.1 角動量算符10...
