泡利方程

泡利方程或稱薛丁格-泡利方程，為描述帶有自旋1/2的粒子在與電磁場相互作用下的修正方程（自旋1/2粒子例如電子）。在此之前，用以描述粒子行為的薛丁格方程則未考慮到粒子自旋的性質。其為狄拉克方程在非相對論極限下的特例，套用在粒子速度慢到相對論效應可以忽略的場合。

泡利方程是由沃爾夫岡·泡利於1927年所建構。

基本介紹

• 中文名：泡利方程
• 外文名：Pauli equation
• 別稱：薛丁格-泡利方程
• 創建人：沃爾夫岡·泡利
• 創建時間：1927年
• 所屬領域：量子力學
• 套用學科：物理學

方程

一自旋粒子具有質量m、電荷q，於外加電磁場中運動；外加電磁場可以標勢ϕ、矢勢A= (A_x,A_y,A_z)來描述。泡利方程可描述外加電磁場與自旋相互作用的影響：

泡利方程（廣義形式）

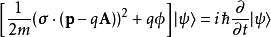
其中

為動量算符（p= −iħ∇，∇為梯度算符），

為泡利矩陣，

為泡利旋量。

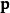
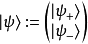
兩個旋量分量都滿足薛丁格方程

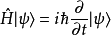
這表示系統是有額外但簡併的的自由度。

另可看出泡利方程的哈密頓算符為：

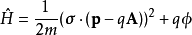
因泡利矩陣的存在，此哈密頓算符為2 × 2矩陣算符。泡利方程的哈密頓算符形似於帶電粒子在電磁場中的經典哈密頓算符，但後者沒有考慮到自旋。

泡利矩陣可以從動能項中移出，只要使用泡利矩陣的關係式：

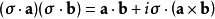
將p= −iħ∇代入，可得到

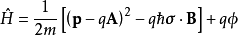
其中B= ∇ ×A，即磁場。

實驗相關

與施特恩-格拉赫實驗的關係：

泡利方程可分拆為兩項：

泡利方程（磁場B）

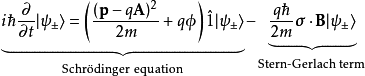
同上述，

為泡利旋量，

為泡利矩陣所構成的泡利矢量，

B為外加磁場，與磁矢勢A的關係為：，

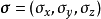
而

為二階單位矩陣。

左半部為薛丁格方程（上式Schrödinger equation），右半部施特恩-格拉赫項（上式Stern-Gerlach term）。如此可解釋帶有一個價電子的原子何以得到得到自旋取向，例如流過不均勻磁場的銀原子。相似地，比如在反常塞曼效應，這一項造成磁場中的譜線（對應到能階）分裂。

方程相關

與薛丁格方程、狄拉克方程的關係：

泡利方程為非相對論性的量子力學方程，但其能描述自旋相關的行為，因此其具有薛丁格方程與狄拉克方程的中介角色：

常見的薛丁格方程（作用於復標量波動方程），非相對論性，也無法描述自旋。

狄拉克方程（作用於複數四分量旋量），完整地考慮了相對論效應，可描述自旋。

注意到：若磁矢勢A為零，泡利方程則約化為一個在純電勢ϕ中運動的帶電粒子之薛丁格方程：

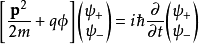
但因為泡利矩陣的存在，此方程是作用在二分量旋量上的。因此僅當磁場存在時，粒子自旋才會對粒子的運動發揮影響。

推導

由狄拉克方程推導泡利方程：

自狄拉克方程開始，設定弱的電磁場相互作用：

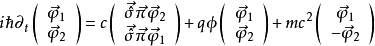
其中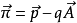

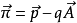
利用到如下近似：

透過如下擬設對方程做簡化

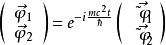
透過緩慢時間相依性的前提去除掉靜能量

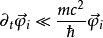
與電場勢有弱的耦合