包立方程式

泡利方程或稱薛丁格-泡利方程，為描述帶有自旋1/2的粒子在與電磁場相互作用下的修正方程（自旋1/2粒子例如電子）。在此之前，用以描述粒子行為的薛丁格方程則未考慮到粒子自旋的性質。其為狄拉克方程在非相對論極限下的特例，套用在粒子速度慢到相對論效應可以忽略的場合。

泡利方程是由沃爾夫岡·泡利於1927年所建構。

基本介紹

• 中文名：包立方程式
• 外文名：Pauli equation
• 領域：量子力學

簡介

泡利方程或稱薛丁格-泡利方程，為描述帶有自旋1/2的粒子在與電磁場相互作用下的修正方程（自旋1/2粒子例如電子）。在此之前，用以描述粒子行為的薛丁格方程則未考慮到粒子自旋的性質。其為狄拉克方程在非相對論極限下的特例，套用在粒子速度慢到相對論效應可以忽略的場合。

泡利方程是由沃爾夫岡·泡利於1927年所建構。

與薛丁格方程、狄拉克方程的關係

泡利方程為非相對論性的量子力學方程，但其能描述自旋相關的行為，因此其具有薛丁格方程與狄拉克方程的中介角色：

• 常見的薛丁格方程（作用於復標量波動方程），非相對論性，也無法描述自旋。
  
• 狄拉克方程（作用於複數四分量旋量），完整地考慮了相對論效應，可描述自旋。
  

注意到：若磁矢勢A為零，泡利方程則約化為一個在純電勢ϕ中運動的帶電粒子之薛丁格方程：

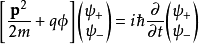
但因為泡利矩陣的存在，此方程是作用在二分量旋量上的。因此僅當磁場存在時，粒子自旋才會對粒子的運動發揮影響。

沃爾夫岡·泡利

沃爾夫岡·歐內斯特·泡利（德語：Wolfgang Ernst Pauli，1900年4月25日－1958年12月15日），奧地利理論物理學家，是量子力學研究先驅者之一。1945年，在愛因斯坦的提名下，他因泡利不相容原理而獲得諾貝爾物理學獎。泡利不相容原理涉及自旋理論，是理解物質結構乃至化學的基礎。

自旋1/2

在量子物理中，自旋½表示一粒子所具有的內稟角動量（自旋）為，是約化普朗克常數，其中包括了電子、質子、中子、中微子與虧子(夸克)。自旋-½粒子在量子統計上屬於費米子，並遵守泡利不相容原理。

對自旋½粒子進行自旋性質的量子測量會得到兩個值。有兩個結果肇因於所存有的矢量空間的維度。自旋½粒子的自旋量子態可以用一種兩個維度的複數值矢量來描述，稱之為二元旋量。利用這種表示法，量子力學中的算符可寫成2乘2(2 x 2)的複數厄米矩陣。

薛丁格方程

在量子力學中，薛丁格方程（Schrödinger equation）是描述物理系統的量子態怎樣隨時間演化的偏微分方程，為量子力學的基礎方程之一，其以發表者奧地利物理學家埃爾溫·薛丁格而命名。關於量子態與薛丁格方程的概念涵蓋於基礎量子力學假說里，無法從其它任何原理推導而出。

在經典力學裡，人們使用牛頓第二定律描述物體運動。而在量子力學裡，類似的運動方程為薛丁格方程。薛丁格方程的解完備地描述物理系統里，微觀尺寸粒子的量子行為；這包括分子系統、原子系統、亞原子系統；另外，薛丁格方程的解還可完備地描述巨觀系統，可能乃至整個宇宙。

薛丁格方程可以分為“含時薛丁格方程”與“不含時薛丁格方程”兩種。含時薛丁格方程與時間有關，描述量子系統的波函式怎樣隨著時間而演化。不含時薛丁格方程則與時間無關，描述了定態量子系統的物理性質；該方程的解就是定態量子系統的波函式。量子事件發生的機率可以用波函式來計算，其機率幅的絕對值平方就是量子事件發生的機率密度。

薛丁格方程所屬的波動力學可以數學變換為維爾納·海森堡的矩陣力學，或理察·費曼的路徑積分表述。薛丁格方程是個非相對論性方程，不適用於相對論性理論；對於相對論性微觀系統，必須改使用狄拉克方程或克萊因-戈爾登方程等。