基本介紹
緒論
定義
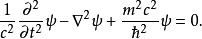

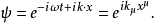
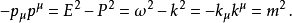
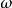
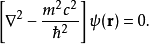
形式推導
相對論量子力學


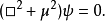
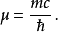

量子場論

自由粒子解

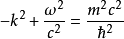

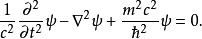

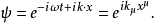
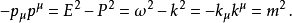
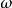
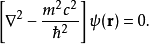


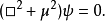
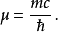



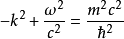
克萊因-戈爾登方程(Klein-Gordon equation)是相對論量子力學和量子場論中的最基本方程,它是薛丁格方程的狹義相對論形式,用於描述自旋為零的粒子。克萊因-戈爾登方程...
克萊因-戈爾登方程(Klein-Gordon equation)是相對論量子力學和量子場論中的最基本方程,用於描述自旋為0的自由標量場的相對論性運動方程。克萊因-戈爾登方程是由瑞典...
理論物理中,相對於薛丁格方程之於非相對論量子力學,狄拉克方程是相對論量子力學...狄拉克場 薛丁格方程 克萊因-戈爾登方程 泡利方程 外爾方程 ...
薛丁格方程是個非相對論性方程,不適用於相對論性理論;對於相對論性微觀系統,必須改使用狄拉克方程或克萊因-戈爾登方程等。 [2] 參考資料 1. Claude Cohen-...
3.2 克萊因-戈爾登方程 3.2.1 薛丁格方程的得出及其缺陷 3.2.2 克萊因-戈爾登方程 3.3 狄拉克方程 3.3.1方程的建立 3.3.2 方程的協變形式 ...
這方程後來稱為克萊因-戈爾登方程。1928年,保羅·狄拉克最先成功地統一了狹義相對論與量子力學,他推導出狄拉克方程,適用於電子等等自旋為1/2的粒子。這方程的波...
當時雖然已經有了克萊因-戈爾登方程,但狄拉克認為問題並未被解決。這個方程可能給出負值的機率,量子力學對機率的詮釋無法解釋這個問題。 狄拉克和泡利 ...
達朗貝爾運算元通常用來表達克萊因-戈爾登方程以及四維波動方程。第四個項前面的符號是負號,而在歐幾里德空間中則是正號。因子c是需要的,這是因為時間和空間通常用不...
在粒子物理學中,量子電動力學(英語:Quantum Electrodynamics,簡稱QED)是電動力學的相對論性量子場論。狄拉克方程與克萊因-戈爾登方程的解,前者描述的是電子機率幅的...
狄拉克所希望建立的是一個同時具有洛倫茲協變性和薛丁格方程形式的波方程,並且這個方程需要確保所導出的機率密度為正值,而不是像克萊因-戈爾登方程那樣存在缺乏物理...
達朗貝爾運算元主要套用在電磁學、狹義相對論中,例如克萊因-戈爾登方程(Klein-Gordon equation)中就有用到達朗貝爾運算元。參考資料 1. The causal Green's function for...
[2] 1926年,在那篇著名的文獻中,奧地利量子物理大師薛丁格提出了不考慮相對論的薛丁格方程。科學家對薛丁格方程作了相對論性的修正(參見克萊因-戈爾登方程),以解釋...
早期,對於合併量子力學與狹義相對論的試圖,涉及到使用協變方程,例如,克萊因-戈爾登方程或狄拉克方程,來取代薛丁格方程。這些方程雖然能夠很成功地描述許多量子現象,但...
