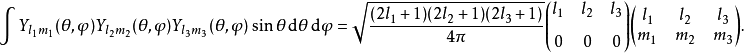克萊布希－高登係數

在量子力學中，克萊布希－高登係數（Clebsch–Gordan

coefficients，簡稱 CG 係數，又稱向量耦合係數等）是兩個角動量耦合時，它們的本徵函式的組合係數。從數學的角度，克萊布希－高登係數出現在緊李群的表示論中，它研究的是兩個不可約表示的張量積如何分解成不可約表示的直和。克萊布希－高登係數因阿爾弗雷德·克萊布希和保羅·哥爾丹而得名。

基本介紹

• 中文名：克萊布希－高登係數
• 外文名：Clebsch–Gordancoefficients
• 又稱：向量耦合係數
• 學科：量子力學
• 定義：角動量耦合時本徵函式的組合係數
• 領域：數學、物理學

定義

從角動量的一般量子理論出發，以角動量算符的對易關係為基礎，不涉及角動量算符在某個具體表象下的表示。給定了j之後，本徵函式組

張開成一個 2j+1 維的函式空間。

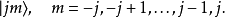
現在給定兩個量子數j₁和j₂，則其本徵函式組張開的空間分別有 2j₁+1 維 與 2j₂+1 維。現考慮這兩個函式空間的張量積：

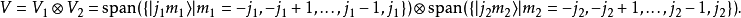
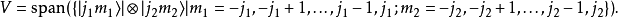
下面為簡便起見，定義新的記號

一般地，若f,g分別是這兩個空間裡的算符，則在積空間上可以定義下列算符：

另一方面，定義在這兩個空間上的算符可以自然地嵌入到積空間中，只需取

其中 1 表示恆等操作（算符）。

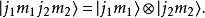
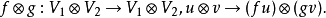
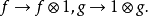
在這樣的定義下，兩個角動量算符的的耦合表達為：

容易驗證這樣定義的j滿足角動量的基本對易關係，因此是一個角動量算符，稱為總角動量算符。

根據角動量的一般理論，總角動量算符也有自己的本徵函式組，它可以用積空間裡的基來表示

這裡的線性組合係數

就被稱為克萊布希－高登係數。在正交歸一性的要求下，克萊布希－高登係數仍然具有相位不確定性。本文中取 Condon-Shortle 慣例，使所有克萊布希－高登係數為實數。

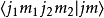
例子

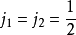以 為例。

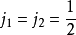
對任意一個算符 f，本節中的矩陣元表示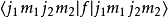 的值。

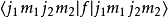
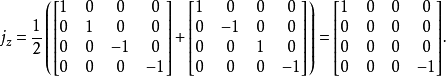
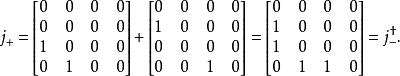
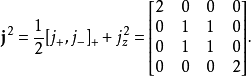
計算最後一個矩陣的本徵值和本徵向量，得到

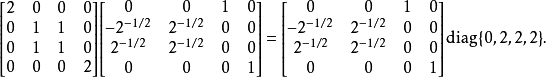
於是可到克萊布希－高登係數。從上面的例子可以看到，對於一般的情況，用矩陣來求克萊布希－高登係數將是十分繁瑣的。一般可以採用下面的 Racah 表達式計算，更多的情況是直接查表。

Racah 表達式

Racah 用代數方法得出了克萊布希－高登係數的有限級數表達式。

其中，ν的求和限制在使得所有的階乘因子中的數非負的範圍內。

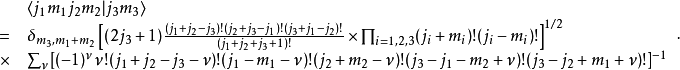
對稱性

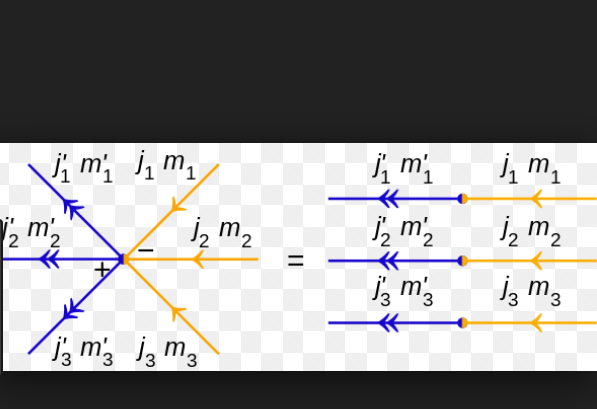
克萊布希－高登係數有下列的對稱性

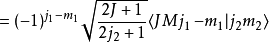
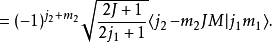
其他關係

克萊布希－高登係數與維格納 3-j符號有下列關係：

後者可以用於計算下列形式的球諧函式積分：

由球諧函式的正交歸一性，上面的結果也可以用來對球諧函式作展開。