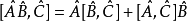對易的算法,即算符的對易關係(Commutation relation)。設F和G為兩個算符,若FG-GF=0,則F和G對易;若FG-GF≠0,則F和G不對易。
基本介紹
- 中文名:對易的算法
- 外文名:Commutation relation
- 解釋:算符的對易的關係
- 學科:數學、量子力學
對易關係,算符的對易關係舉例,
對易關係
引入對易子 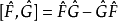 :
:
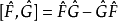
若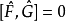 ,則
,則 和
和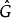 對易;
對易;
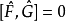

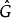
若 ,則
,則 和
和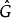 不對易;
不對易;


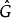
對易式滿足下列恆等式:(設 表示算符)
表示算符)

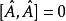
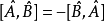
雙線性:


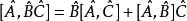

算符的對易關係舉例
關於對易關係,一個很常見的例子就是量子力學中,坐標算符與動量算符的對易關係(考慮一維情形):
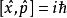
其中坐標算符即左乘 ,動量算符則為
,動量算符則為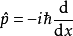

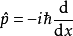
證明:引入測試函式 ,將對易子作用於該函式得到
,將對易子作用於該函式得到

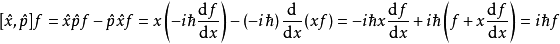
可見這個對易子作用於該函式就相當於該函式左乘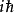 ,這時我們就說坐標算符與動量算符的對易關係為
,這時我們就說坐標算符與動量算符的對易關係為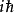 ,記作
,記作
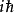
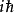
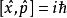
通過上述例子可知,對易的算法即引入一個測試函式(比如 ,一般對測試函式的要求是連續可導),然後將對易子作用於測試函式展開進行算符運算,算符運算的次序從左到右,最後得到的結果中必定可以用原函式表示,再把這個測試函式從兩端消去(即將算符抽象出來,並不等價於簡單的除法),得到的就是算符的對易關係。
,一般對測試函式的要求是連續可導),然後將對易子作用於測試函式展開進行算符運算,算符運算的次序從左到右,最後得到的結果中必定可以用原函式表示,再把這個測試函式從兩端消去(即將算符抽象出來,並不等價於簡單的除法),得到的就是算符的對易關係。