熱力學（thermodynamics）是從巨觀角度研究物質的熱運動性質及其規律的學科。屬於物理學的分支，它與統計物理學分別構成了熱學理論的巨觀和微觀兩個方面。
熱力學主要是從能量轉化的觀點來研究物質的熱性質 ，它揭示了能量從一種形式轉換為另一種形式時遵從的巨觀規律，總結了物質的巨觀現象而得到的熱學理論。熱力學並不追究由大量微觀粒子組成的物質的微觀結構，而只關心繫統在整體上表現出來的熱現象及其變化發展所必須遵循的基本規律。它滿足於用少數幾個能直接感受和可觀測的巨觀狀態量諸如溫度、壓強、體積、濃度等描述和確定系統所處的狀態。通過對實踐中熱現象的大量觀測和實驗發現，巨觀狀態量之間是有聯繫的，它們的變化是互相制約的。制約關係除與物質的性質有關外，還必須遵循一些對任何物質都適用的基本的熱學規律，如熱力學第零定律、熱力學第一定律、熱力學第二定律和熱力學第三定律 等。熱力學以上列從實驗觀測得到的基本定律為基礎和出發點，套用數學方法，通過邏輯演繹，得出有關物質各種巨觀性質之間的關係和巨觀物理過程進行的方向和限度，故它屬於唯象理論，由它引出的結論具有高度的可靠性和普遍性。
基本介紹
- 中文名：熱力學
- 外文名：thermodynamics
- 全稱：熱動力學
- 研究內容：巨觀物質的熱運動性質及其規律
- 學科性質：物理學的分支
- 特徵：遵循熱力學定律
發展簡史,定義態函式,平衡態特性,第零定律和溫度,第一定律和內能,可逆和不可逆過程,第二定律和熵,第三定律和絕對熵,不可逆過程,系統分類,開放系統,封閉系統,孤立系統,局限性,相關學科,
發展簡史
古代人類早就學會了取火和用火，但是後來才注意探究熱、冷現象本身，直到17世紀末還不能正確區分溫度和熱量這兩個基本概念的本質。在當時流行的“熱質說”統治下，人們誤認為物體的溫度高是由於儲存的“熱質”數量多。1709—1714年華氏溫標和1742—1745年攝氏溫標的建立，才使測溫有了公認的標準。隨後又發展了量熱技術，為科學地觀測熱現象提供了測試手段，使熱學走上了近代實驗科學的道路。1798年，馮·朗福德觀察到用鑽頭鑽炮筒時，消耗機械功的結果使鑽頭和筒身都升溫。1799年，英國人H.戴維用兩塊冰相互摩擦致使表面融化，這顯然無法由“熱質說”得到解釋。1842年，J.邁爾提出了能量守恆理論，認定熱是能的一種形式，可與機械能互相轉化，並且從空氣的定壓比熱容與定容比熱容之差計算出熱功當量。英國物理學家J.焦耳於1840年建立電熱當量的概念，1842年以後用不同方式實測了熱功當量。1850年，焦耳的實驗結果已使科學界徹底拋棄了“熱質說”，公認能量守恆 、而且能的形式可以互換的熱力學第一定律為客觀的自然規律。能量單位焦耳（J）就是以他的名字命名的。
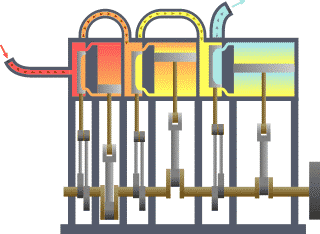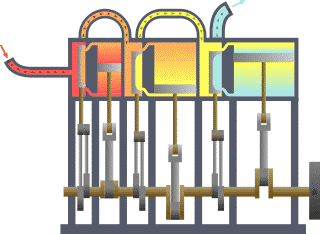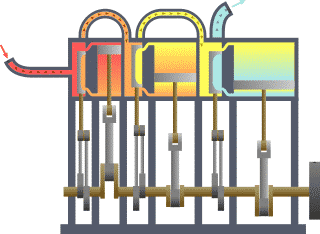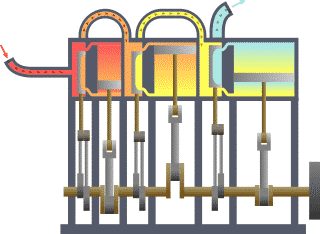
一個典型的熱力學系統
熱力學的形成與當時的生產實踐迫切要求尋找合理的大型、高效熱機有關。1824年，法國人S.卡諾提出著名的卡諾定理，指明工作在給定溫度範圍的熱機所能達到的效率極限，這實質上已經建立起熱力學第二定律，但受 “熱質說”的影響，他的證明方法還有錯誤。1848年，英國工程師開爾文（即W.湯姆森）根據卡諾定理制定了熱力學溫標。1850年和1851年，德國的R.克勞修斯和開爾文先後提出了熱力學第二定律，並在此基礎上重新證明了卡諾定理。1850—1854年，克勞修斯根據卡諾定理提出並發展了熵。熱力學第一定律和第二定律的確認，對於兩類 “永動機”的不可能實現作出了科學的最後結論，正式形成了熱現象的巨觀理論熱力學。與此同時，在套用熱力學理論研究物質性質的過程中，還發展了熱力學的數學理論，找到反映物質各種性質的相應熱力學函式，研究了物質在相變、化學反應和溶液特性方面所遵循的各種規律。1906年，德國的W.能斯脫在觀察低溫現象和化學反應中發現熱定理。1912年，這個定理被修改成熱力學第三定律的表述形式。20世紀初以來，對超高壓、超高溫水蒸汽等物性和極低溫度的研究不斷獲得新成果。隨著對能源問題的重視，人們對與節能有關的複合循環、新型的複合工質（包括製冷劑或冷媒）的研究發生了很大興趣。
定義態函式
熱力學在系統平衡態概念的基礎上，定義了描述系統狀態所必須的三個態函式：熱力學溫度T、內能U和熵S。熱力學第零定律為定義和標定溫度奠定了基礎；熱力學第一定律定義了態函式內能；第二定律引進了態函式熵和熱力學溫標；熱力學第三定律則描述了系統的內能和熵在絕對零度附近的性狀。
平衡態特性
系統的狀態是由其全部的狀態參量及其變化來加以確定的。經驗證明，沒有外界影響的條件下，系統的各部分的巨觀性質總會趨向一個長時期不發生變化的狀態，稱為平衡態。只當系統處於平衡態時，其狀態參量才有確定的數值和意義。處於平衡態的定量系統，其狀態參量之間存在確定的函式關係，表示這種函式關係的數學關係稱為該系統的狀態方程。對於不受外場作用並處於平衡態的單元均勻系，為描述和確定系統所處的狀態只需三個狀態參量，它們是溫度T、體積V和壓強p，故狀態方程為F(T,V,p)=0。說明為了確定這樣的系統所處於的狀態，只有兩個狀態參量是獨立的，它們可是(p,V)，也可是(p,T)或(T,V)。一切可用來描述和確定系統所處狀態並是系統獨立狀態參量單值函式的物理量稱為系統的狀態函式或態函式。如對於一個單元均勻系，取(p,V)作為獨立的狀態參量時，溫度T就是態函式。熱力學中常用的態函式有內能U、焓H、熵S、自由能F和自由焓G等。
第零定律和溫度
溫度是物體冷熱程度的數值表示。經驗證明，達到熱平衡的兩物體的溫度相等；若把已經達到熱平衡的兩物體分開，則物體的狀態將維持不變。為了判別兩個物體溫度的高低，必須引進第三個物體，並依據基本實驗事實 ：若兩個物體分別與處於確定狀態的第三個達到熱平衡，則這兩個物體彼此也處於熱平衡。由於此實驗事實是標定物體溫度數值的基本依據，故稱為熱力學第零定律。
第三個物體的溫度變化通常是通過該物體的某一個可觀測的物理性質的變化加以標誌的。但此性質必須隨物體的冷熱程度有顯著和單值的變化。如以液體體積變化作為溫度變化標誌的液體溫度計，以氣體壓強、氣體體積、電阻、溫差電勢和光的亮度等作為溫度變化標誌的定壓氣體溫度計、定容氣體溫度計、電阻溫度計、熱電偶溫度計和光學高溫計等。溫度數值的標定方法稱為溫標，溫標按其標定溫度方法的不同，可分為經驗溫標、理想氣體溫標和熱力學溫標。
第一定律和內能
熱力學第一定律確認：任何系統中存在單值的態函式——內能，孤立系統的內能恆定。一個物體的內能是當物體靜止時，組成該物體的微觀粒子無規則熱運動動能以及它們之間的相互作用勢能的總和。巨觀定義內能的實驗基礎是，系統在相同初終態間所做的絕熱功數值都相等，與路徑無關。由此可見，絕熱過程中外界對系統所做的功只與系統的某個函式在初終態之間的改變有關，與路徑無關。這個態函式就是內能。它可通過系統對外界所做的絕熱功As加以定義：U2－U1=－As，式中的負號表示對外做功為正功。功的單位是焦耳。在一個純粹的熱傳遞過程中，可用系統的內能改變來定義熱量及其數值，即Q=U2－U1，這裡定義系統吸熱為正（Q大於0）。熱量的單位也是焦耳。
一般情況下熱力學第一定律可表述為：系統由初態出發經任意過程到達終態，內能的增量ΔU等於在此過程中外界對系統所傳遞的熱量Q和系統對外所作的功A之差。數學表達式可寫為：
ΔU=U2－U1=Q－A或Q=ΔU+A
其中規定：系統吸熱Q>0，系統放熱Q<0；系統對外做功A>0，外界對系統做功A<0；系統內能增加ΔU>0，系統內能減少ΔU<0。把上式套用於相差無窮小的兩狀態間發生的微元過程，可得熱力學第一定律的微分形式：
δQ=dU+δA
式中的dU是內能的全微分；δQ和δA分別表示微元過程中傳遞的微熱量和對外所做的微功，它們都不是全微分。
熱力學第一定律還可表述為第一類永動機（一種能不斷自動做功而無須消耗任何燃料和能源的機器）是做不成的。
當系統是開放的，它和介質之間不僅有熱的和機械的相互作用，還有物質交換，則熱力學第一定律的表述中還應增加一項因物質交換引起的能量的增量或減量。
可逆和不可逆過程
熱力學系統的狀態隨時間的變化叫作熱力學過程，簡稱過程。每一時刻系統都處於平衡態的過程叫準靜態過程或準平衡過程。如果一個過程既可正向進行，也可逆向進行，而且在逆過程時系統經過的全部狀態與正過程所經歷的狀態相同只是次序相反，並在每一步上消除了正過程在外界產生的影響，則原過程稱為可逆過程。若無論用什麼辦法都不能消除正過程在外界產生的影響，則原過程稱為不可逆過程。
事實上，沒有摩擦阻力和其他損失的準靜態過程一定是可逆的過程。如氣缸中的理想氣體在活塞作用下完成準靜態的等溫膨脹過程，過程中氣體對外界做功和同時從恆溫熱源吸取熱量分別為W和Q；達到終態後，若讓活塞緩慢地反向運動，完成準靜態的等溫壓縮過程，則過程將一步步地沿原過程經歷的狀態進行，只是方向相反，而且在每一步上外界對系統做功和系統向恆溫熱源放出熱量的數值，恰好分別等於正過程時系統所做的功和從熱源吸收的熱量，並消除了原過程在外界產生的一切影響。從而說明，無摩擦和其他損失的準靜態過程是可逆過程。
不可逆過程的例子有向真空的自由膨脹過程（即氣體起初只占據容器的一部分，然後充滿其餘原為真空的部分）；溫度不同的兩物體，通過熱接觸達到熱平衡的過程。因為這些過程都不能在不引起外界影響的情況下而恢復原狀。嚴格地講，一切由大量粒子組成的系統中發生的巨觀過程都是不可逆的，因為在機械運動中總伴隨著摩擦損失；熱傳遞過程中熱量總是從較熱的部分傳到較冷的部分。這些過程中總的能量仍是守恆的，並不違反熱力學第一定律。因此，必然存在另外一些基本規律，它們將對實際過程可進行的方向作出限定。這就是熱力學第二定律，以及在此基礎上引進的態函式熵。
第二定律和熵
經驗指出熱功轉換是不可逆的，熱功轉換不可逆性可以在大量的熱機循環中觀察到，無法製成一個只從高溫熱源吸熱而不放熱到低溫熱源的循環動作的熱機。經過總結大量實踐得到結論：不可能從單一熱源吸取熱量，使之完全變為有用的功而不產生其他影響。這就是熱力學第二定律的開爾文表述。它否定了製作第二類永動機（見永動機）的可能性。除熱功轉換不可逆性外，熱量傳遞也是不可逆的：熱量總是自發地從高溫物體傳遞到低溫物體，而相反的過程是不可能自發地進行的。在大量實驗的基礎上，克勞修斯總結出熱力學第二定律另一種表述：不可能把熱量從低溫物體傳遞到高溫物體而不產生其他影響。
巨觀態出現的機率與它包含的微觀態的數目有關。一種巨觀態所對應的微觀態的數目稱為熱力學機率。熱力學機率越大，這種巨觀態在實驗中被觀測到的機會越多。平衡態是熱力學機率W最大的巨觀態，具有確定的數值 ，故若用玻耳茲曼公式定義平衡態的熵為S=klnW，則系統中自發進行的由機率較小的狀態過渡到機率較大的狀態的不可逆過程是一個熵增加的過程，從而在微觀上解釋了熵增加原理。
第三定律和絕對熵
熱力學第三定律是指限定溫度趨於絕對零度時物質性質變化必須遵循的基本規律。它是在大量實驗觀測基礎上概括而成的，主要內容是能斯特定理和由它引出的絕對零度不可達原理。
由能斯特定理可知，凝聚系的熵將隨熱力學溫度趨向零而趨向一個常數值S0。為了確定這個熵常數，M.普朗克於1911年提出了一個假設S0=0。由此確定的熵的數值稱作絕對熵。由於熱容是正定的，因此系統絕對熵S≥0。普朗克的假設能從近代量子論中找到合理的解釋：達到平衡態絕對零度的系統處於能量最小的狀態。這是一種高度有序的狀態，與之相應的熱力學機率W=1，故套用玻耳茲曼熵公式可得S0=0。
1912年能斯特又從能斯特定理引出一個結論：不可能使一個物體通過有限數目的手續冷卻到絕對零度。這就是著名的絕對零度不可達原理。
不可逆過程
遠離平衡區的情況遠比線性非平衡區遇到的情況要複雜，此時非平衡系統中的力和流之間的關係通常是非線性的，可把這個區域稱為非線性區。流體動力學、化學和生命科學中面臨的大量前沿問題，恰是遠離平衡的和非線性的問題。故對遠離平衡區的不可逆過程熱力學理論及其套用的研究，在國際上引起很大的關注和興趣。事實上任何生命結構包括它的基本單元（細胞）都是處於極端非平衡狀態的開放的熱力學系統。遠離平衡區不可逆過程熱力學研究在這些領域取得的重要進展，使之成為當代物理學發展迅速的分支之一。
理論分析表明，對於近平衡區由演變的通用法則可導出熵產生最小原理，所以系統是穩定的；但對於遠離平衡的非線性區的系統，就不總是穩定的。存在一個臨界態，稱為分支點，系統在越過分支點後，任意小的擾動譬如說漲落都可能誘發系統從穩定到不穩定態的突變，在其中呈現出新的時空有序結構。普里戈金等把這種有序結構稱為耗散結構，這種現象叫自組織現象。如1900年H.貝納德在非均勻加熱的流體中觀察到的有序六角形對流格子和流體在高雷諾數區出現的從層流向湍流結構的轉變等現象，其中都可觀察到大量分子團的有序運動。化學反應的遠離平衡區觀測到的非均勻和準周期性的混合物的空間有序結構和可能出現的反應時序是在空間和時間上呈現出來的耗散結構和自組織現象的重要例證。
系統分類
開放系統
系統與環境之間存在能量和物質傳遞。
封閉系統
孤立系統
系統與環境之既無能量傳遞，又無物質傳遞。
