技術原理
除了上面所述,流體還假設遵守“
連續性假設”(continuum assumption)。流體由
分子所組成,彼此互相碰撞,也與
固體相碰撞。然而,
連續性假設考慮了流體是連續的,而非離散的。因此,諸如密度、壓力、溫度以及速度等性質都被視作是在無限小的點上具有良好定義的,並且從一點到另一點是連續變動。流體是由
離散的分子所構成的這項事實則被忽略。
若流體足夠緻密,可以成為一連續體,並且不含有離子化的組成,速度相對於
光速是很慢的,則
牛頓流體的動量方程為“
納維-斯托克斯方程”。其為
非線性微分方程,描述流體的流所帶有的
應力是與
速度及
壓力呈線性相依。未簡化的納維-斯托克斯方程並沒有一般閉形式解,所以只能用在
計算流體力學,要不然就需要進行簡化。
方程可以通過很多方法來簡化,以容易求解。其中一些方法允許適合的流體力學問題能得到閉形式解。
除了質量、動量與能量守恆方程之外,另外還有
熱力學的
狀態方程,使得壓力成為流體其他熱力學變數的函式,而使問題得以被限定。
組成內容
流動穩定性:不可壓縮流動、 可壓縮流動、
粘性流動、無粘流動
研究點
應力張量
根據無粘性流體對於剪下變形沒有抗拒能力和靜止流體不能承受剪應力的事實可以斷言:在無粘性流體或靜止流體中,剪應力為零,而正應力(即法向應力)pxx=pyy=pzz=-p。p稱為無粘性流體或靜止流體的壓力函式,它表征無粘性流體或靜止流體在任一點的應力狀態。在流體動力學中可以用px、py、pz或九個量pij(i,j=1,2,3)的組合可完全地描寫一點的應力狀況。pij組成的二階張量稱為應力張量。
應力張量和變形速率張量的關係
牛頓粘性定律
只適用於剪下流動(見牛頓流體)。對於一般的流動,假設:(1)運動流體的應力張量在運動停止後趨於靜止流體的應力張量,於是
,式中p
ij為應力張量;p為壓力;δ
ij為克羅內克符號;
為偏應力張量(2)偏應力張量的各分量是速度梯度張量
各分量的線性齊次函式(這個假設是牛頓粘性公式邏輯上的推廣);(3)流體是各向同性的。由此可以推出應力張量和變形速率張量s
ij的關係:
動量方程和能量方程
動量方程是動量守恆的數學表達式,它的矢量形式為:
式中v為速度矢量;F為作用在單位質量上的質量力;p為壓力;ρ、μ分別為流體密度和動力粘性係數。上式表明單位體積上的慣性力等於單位體積上的質量力加上單位積上的壓力梯度和粘性應力。能量方程是能量守世的數學表達式,它可以寫成;
式中T、s分別為流體的熱力學溫度和單位質量流體的熵;k為熱導率;q為由於輻射或其他原因在單位時間內傳入單位質量流體中的熱量;Φ為粘性耗損函式,其表達式為
渦旋的動力學性質
渦旋的動力學性質主要體現在開爾文定理和亥姆霍茲定理上。如果流體是無粘性、正壓的(見正壓流體),且外力有勢,則渦旋不生不滅,而且渦線、渦管總是由相同的流體質點組成,渦管強度不隨時間變化。只有流體的粘性、斜壓性和外力無勢這三個因素才能使渦旋產生、發展變化和消亡.
伯努利積分和拉格朗日積分
無粘性的、正壓的流體在有勢外力作用下,其運動方程在定常和無旋兩特殊情形下可以積分出來。運動方程的這兩個第一積分分別稱為伯努利積分(見伯努利定理)和拉格朗日積分。它們(特別是伯努利積分)無論在流體力學的理論研究或實際套用上都十分有用。
動量定理
對於大部分流體力學問題,為了了解整個流場的情況,需要在一定的初始條件和邊界條件下解微分形式的流體力學基本方程組。但是,有時只需要知道某些整體性的特徵量(例如流體對於在其中運動著的物體的反作用力和整個流動系統的能量損失等),就可以利用積分形式方程組中的整體性定理——動量定理和動量矩定理,根據邊界上給定的流動參數直接求出感興趣的特徵量,而不需要解微分方程。上述方法簡單易行,在流體動力學中有著廣泛的套用。
主要種類
可壓縮流與不可壓縮流
所有流體某種程度上而言都是可壓縮的,換言之,壓力或溫度的改變會造成流體密度的改變。然而,許多情況下,壓力或溫度改變所造成的密度改變相當微小,是可以被忽略的。此種流體可以用不可壓縮流進行模擬,否則必須使用更普遍性的可壓縮流
方程式進行描述。
數學上而言,不可壓縮性代表著流體流動時,其密度維持不變,換言之:其中,D / Dt為對流導數(convective derivative)。此條件可以簡化許多描述流體的
方程式,尤其是運用在均勻密度的流體。
對於氣體要辨別是否具有可壓縮性,馬赫數是一個衡量的指標。概略來說,在
馬赫數低於0.3左右時,可以用
不可壓縮流的行為解釋。至於液體,較符合可壓縮流還是
不可壓縮流的性質,主要取決於液體本身的性質(特別是液體的臨界壓力與臨界溫度)和流體的條件(液體壓力是否接近和液體臨界壓力)。 聲學的問題往往需要引進壓縮性的考量,因為
聲波算是可壓縮波,其性質會隨著傳播的介質以及壓力變化而改變。
黏性流與非黏性流
當流體內的阻力越大時,描述流體須考慮其黏性的影響。
雷諾數可用來估算流體的黏性對描述問題的影響。所謂史托克流指
雷諾數相當小的流動。在此情況,流體的
慣性相較於黏性可忽略。而流體的
雷諾數大代表流體流動時
慣性大於黏性。因此當流體有很大的
雷諾數,假設它是非黏性流,忽略其黏性,可當成一個近似。 這樣的近似,當
雷諾數大時,可得到很好的結果。即使在某些不得不考慮黏性的問題(例如邊界問題)。在流體與管壁的邊界,有所謂的不滑移條件,局部會有很大的速率
應變率,使得黏性的作用放大而有渦度,黏性因而不可被忽略。 因此,計算管壁對流體的
淨力,需要使用黏性
方程式。如同達朗白
謬論的說明,物體在非黏性流里,不會感受到力。尤拉
方程是描述非黏性流的標準
方程式。在這種情況,一個常使用的模型,使用尤拉
方程描述遠離邊界的流體,在接觸的邊界,使用
邊界層方程式。 在某一個流線上,將尤拉
方程積分,可得到白努利方程。如果流體每一處都是無旋轉渦動,白努利
方程可描述整個流動。
 流體動力學
流體動力學穩定流與非穩定流
流體速度和壓力隨時間而改變的流動稱為非穩定流。非穩定流的速度和壓力不僅要考慮位置,同時也要考慮時間的影響。流體速度和壓力均不隨時間而改變的流動稱為穩定流。
層流亂流
當流動由漩渦和明顯的隨機性所主導時,此種流動稱為亂流。當亂流效應不明顯時,則稱為層流。然而值得注意的是,流動之中存在於漩渦不一定表示此流動為亂流──這些現象可能也存在於層流之中。
數學上,亂流通常以雷諾分離法來表示,也就是亂流可以表示成穩定流與擾動部分的和。亂流遵守納維-斯托克斯方程式。數值直解法(Direct numerical simulation,DNS),基於納維-斯托克斯方程式可套用在
不可壓縮流,可使用
雷諾數對亂流進行模擬(必須在電腦性能與演算結果準確性均能負荷的條件下)。而此數值直解法的結果,可以解釋所得的實驗資料。
然而,大部分我們有興趣的流動都是
雷諾數比DNS能夠模擬的範圍大上許多,即使電腦性能在接下來的數十年間持續發展,仍難以實行模擬。任何飛行交通工具,要足夠能承載一個人(L >3 m)以72 km/h (20 m/s)的速度移動,此情況都遠遠在DNS能夠模擬的範圍之外(
雷諾數為4百萬)。像是空中巴士A300或波音747這類的飛行工具,機翼上的
雷諾數超過4千萬(以翼弦為標準)。為了能夠處理這些生活上實際的問題,需要建立亂流模型。雷諾平均納維-斯托克斯方程式(Reynolds-averaged Navier-Stokes equations) 結合了亂流的效果,提供了一個亂流的模型,將額外的
動量傳遞表示由
雷諾應力所造成;然而,亂流也會增加熱傳與質傳速度。大渦數值模擬計算(Large eddy simulation,LES)也是一個模擬方法,外觀與分離
渦流模型(detached eddy simulation, DES)甚相似,是一種亂流模擬與大渦數值模擬計算的結合。
套用領域
流體動力學研究的對象是運動中的流體(流體指液體和氣體)的狀態與
規律。 流體動力學底下的國小科包括有
空氣動力學(研究氣體)和 hydrodynamics(研究液體)
 流體動力學的套用
流體動力學的套用流體動力學(Fluid dynamics)是
流體力學的一門子學科。
流體動力學有很大的套用,在預測天氣,計算飛機所受的
力和
力矩,輸油管線中石油的流率等方面。其中的的一些原理甚至運用在交通工程。交通運輸本身被視為一連續流體,解決一個典型的流體動力學問題,需要計算流體的多項特性,包括
速度,
壓力,
密度,
溫度。
參考文獻
1.詞條作者:吳望一《中國大百科全書》74卷(第二版)物理學詞條:流體力學:中國大百科全書出版社,2009-07:263-264頁
2.G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge Univ. Press, London, 1970.
3.L. 普朗特等著,郭永懷、陸士嘉譯:《流體力學概論》,科學出版社,北京,1981。(L. Prandtl, et al., Führer Dvrch die Strömungslehre, Friedr. Vieweg und Sohn, Braunschweig, 1969.)
4.吳望一編著:《流體力學》,北京大學出版社,北京,1982。





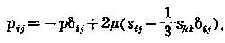

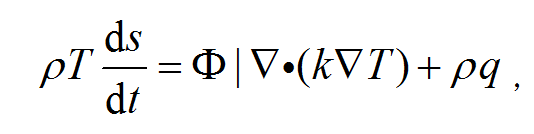

 流體動力學
流體動力學 流體動力學的套用
流體動力學的套用