雷諾傳輸定理(Reynolds transport theorem),又稱為傳輸方程式(Transport equation),用於描述流體(fluid)性質的變化。
基本介紹
- 中文名:雷諾傳輸定理
- 外文名:Reynolds transport theorem
- 又名:傳輸方程式
- 意義:描述流體(fluid)性質的變化
簡介,特點,通用型式,針對流體塊的形式,錯誤的引用,特別形式,簡化,在一維下的詮釋及簡化,
簡介
雷諾傳輸定理也稱為萊布尼茲-雷諾傳輸定理或雷諾定理,是以積分符號內取微分聞名的萊布尼茲積分律的三維推廣。
考慮在時變的區域 積分
積分 ,其邊界為
,其邊界為 ,考慮上式對時間的積分:
,考慮上式對時間的積分:




若要求上述積分的導數,會有兩個問題, 的時間相依性,及因
的時間相依性,及因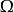 動態的邊界而增加或減少的空間,雷諾傳輸定理提供了必要的框架。
動態的邊界而增加或減少的空間,雷諾傳輸定理提供了必要的框架。

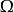
特點
傳輸方程式可用來定量地描述流場中流體性質的變化情形,譬如在一個控制容積(Control volume)之中含有某種流體。在經過一段時間 之後,若控制容積中流體的總體性質B有所改變,則其變化必定是下列兩種原因所造成的: (1)總體性質B可能會因為本身的特性或外在因素的影響而產生隨時間的變化,譬如流體中含有某種化學物質,該物質會因化學反應造成其質量B的變化,dB/dt即為該物質質量的變化率。又譬如B為流體的動量,在受到外力的狀況下,流體的動量會有所改變。 (2)因為流體流動所造成的變化:當流體流經控制容積時,會帶入或帶出一部份的物質。當流出控制容積的總體性質大於流入量,則淨流出量為正,會造成控制容積之中該總體性質的減少;反之,流入量大於流出量便會造成該總體性質的增加。
通用型式
要推導的雷諾傳輸定理是:

其中 為向外的單位法向量,
為向外的單位法向量, 為區域中的一點,也是積分變數,
為區域中的一點,也是積分變數, 及
及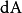 是
是 內的體積元素及表面元素,
內的體積元素及表面元素,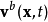 為面積元素的速度,不一定要是流速。函式
為面積元素的速度,不一定要是流速。函式 可以是張量、向量或標量函式。注意等式左邊的積分只是時間的函式,因此可以用全微分。
可以是張量、向量或標量函式。注意等式左邊的積分只是時間的函式,因此可以用全微分。



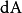

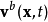

針對流體塊的形式
在連續介質力學中,此定理常用在沒有物質進來或離開的流體塊或固體中。若 為一流體塊,則存在速度函式
為一流體塊,則存在速度函式 及邊界元素符合下式:
及邊界元素符合下式:



上式在替代後,可以得到以下的定理:

錯誤的引用
此定理常被錯誤的引用為只針對物質體積(material volume)的形式,若將只針對物質體積套用於物質體積以外的區域中,就會出現問題。
特別形式
簡化
若 不隨時間改變,則
不隨時間改變,則 ,且恆等式化簡為以下的形式:
,且恆等式化簡為以下的形式:


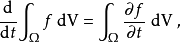
不過若用了不正確的雷諾傳輸定理,無法進行上述的簡化。
在一維下的詮釋及簡化
此定理是積分符號內取微分的高維延伸,有些情形下可以簡化為積分符號內取微分。假設f和y}和z無關,且 為
為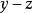 平面的單位方塊,且有
平面的單位方塊,且有 及
及 的極限,雷諾傳輸定理會簡化為:
的極限,雷諾傳輸定理會簡化為:

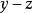



上述是由積分符號內取微分來的表示式,但x及t變數已經對調。
