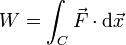功(力和力在力的方向上通過位移的乘積)

功(力和力在力的方向上通過位移的乘積)

本詞條是多義詞，共2個義項
更多義項 ▼ 收起列表 ▲

功（英語：work），也叫機械功，是物理學中表示力對物體作用的空間的累積的物理量，功是標量，其大小等於力與其作用點位移的標積，國際單位制單位為焦耳。“功”一詞最初是法國數學家賈斯帕-古斯塔夫·科里奧利創造的。

基本介紹

  • 中文名：功
  • 外文名：work
  • 又名：機械功
  • 公式：W=Fscosα
定義,解釋,單位,內容,轉矩和轉動,力與位移,力矩,力與位移,比較做功的快慢,與能的關係,內容,常力的功,變力的功,力偶的功,參考文獻,

定義

功（英語：work），也叫機械功。如果一個物體受到力的作用，並在力的方向上發生了一段位移，我們就說這個力對物體做了功。功是物理學中表示力對位移的累積的物理量。與機械能相似的是，功也是標量，國際單位制單位為焦耳。1J=1N·m=1kg·m2·s-2“功”一詞最初是由法國數學家賈斯帕-古斯塔夫·科里奧利創造。
功的定義（一維）
在一維運動（即在一條直線上的運動）中，如果物體因為力F從A運動到B，位移了x，物體做了W的功。
定義
為F在一小段位移dx下做的功為dW。
兩端積分：
，這是功的一般定義。
根據牛頓第二定律：
速度定義式：
(可以理解為在一小段時間內的平均位移為dx，當dt趨於0時，v是瞬時速度）
加速度定義式：
（可理解為在小段時間dt內的平均速度為dv，當dt趨於0時，a是瞬時加速度）
積分可代換為
。（其中
和
分別是物體在A點和B點的速度）
因此，功可以用速度和質量來描述，這樣描述的功我們稱之為總功，因此總功只與物體的質量和初末速度有關，而與物體位移的方式無關。由此，我們有以下結論：
在一維運動中：
如果物體做勻速運動，那么物體總功為零；
如果物體受到的力合力為F，而初運動和末運動的位移方向與F相同，那么這個物體總功大於零；
如果物體受到的力合力為F，而初運動和末運動的位移方向與F相反，那么這個物體總功小於零；
注意：總功和某力的功是有區別的，不能混淆。
功的定義（三維）
在三維運動（即在一個空間中的運動）中，如果物體因為力F從A運動到B，位移了r，物體做了W的功,
r=ix+jy+kz,F=iFx+jFy+kFz，i,j,k分別是x,y,z的正方向單位向量，定義
為物體從A到B所做的功。
根據牛頓第二定律：
速度定義式：
加速度定義式：
我們把三維運動分解為三個方向的一維運動，就有計算公式：
速度的x，y，z正方向的投影用下標表示。
特別的當所有矢量的z方向為0時，是二維運動的總功，如果y方向也為0時，是一維運動的總功，與之前的定義是不矛盾的。
功的公式
W=Fscosα (國中階段，力方向與位移方向的夾角為0，即α=0°，cos0°=1，所以W=Fs)
推導：
在二維運動中，
F是恆定力（即始終不改變的力），s是物體位移，從A到B，α是F與x軸夾角，θ是s與x軸夾角，如果我們令θ=0，那么只需要取s是正方向，垂直於s的是y軸就可以了，那么第二項就為0，AB=s=x，故
做功的兩個因素：
1.作用在物體上的力
2.物體在這個力的方向上移動的距離
註：功的公式只能計算一個力或一個合力所做的功，如要算總功，需用速度與質量的公式。

解釋

如果一個力作用在物體上，物體在這個力的方向上移動了一段距離，力學裡就說這個力做了功。 即使存在力，也可能沒有做功。例如，在勻速圓周運動中，向心力沒有做功，因為做圓周運動的物體的動能沒有發生變化。同樣的，桌上的一本書，儘管桌對書有支持力，但因沒有位移而沒有做功。
總的來說不做功的情況有三種：不勞無功、有勞無功和垂直無功。（不勞無功：只移動了距離，但在這移動的方向上沒產生力，即0*Fs·cosα=0焦耳；有勞無功：只有力，卻在力的方向上沒有移動一定的距離，F*0scosα=0焦耳；垂直無功：物體既受到力，又通過一段距離，但兩者方向互相垂直，Fscos90°=Fs*0=0焦耳。）
熱傳導不被認為是做功，因為能量被轉化成了微觀原子的振動而非巨觀的位移。
PS：功的實質就是力的空間累積。
力與物體在力的方向上通過的距離的乘積稱為機械功（mechanical work)，簡稱功。
功功
功定義為力與位移的內積。其中，W 表示功，F 表示力，而dx 表示與外力同方向的微小位移；上式應表示成路徑積分，a 是積分路徑的起始點，b 是積分路徑的終點。為了了解物體受力作用，經過一段距離後所產生的效應，而定義出功的概念。
功是標量，所以功的正、負不表示方向。功的正負也不表示功的大小。它僅僅表示是動力對物體做功還是阻力對物體做功，或者說是表示力對物體做了功還是物體克服這個力做了功。若要比較做功的多少，則要比較功的絕對值，絕對值大的做功多，絕對值小的做功少。功是能量變化的量度，做功的多少反映了能量變化的多少，功的正負則反映了能量轉化的方向（注意：不是空間的方向）
判斷一個力對物體是否做功，可根據該力和物體位移方向的夾角是否為90°，或力與物體速度方向的夾角是否總是90°來確認力是否對物體做功。夾角大於90°時功為負，夾角小於90°時功為正。所以力的作用是相互的。距離是兩物體之間的差。機械功W=Fs。

單位

國際單位制中功的單位為焦耳（J）。焦耳被定義為用1牛頓的力對一物體使其發生1米的位移所做的機械功的大小。量綱相同的單位牛·米有時也使用，但是一般牛·米用於力矩，使其跟功和能區別開。
在國際單位中，功的單位是焦耳，簡稱‘焦’，符號為J，單位為J 1J=1N·m 由英國物理學家焦耳（James Prescott joule，1818~1889）對科學的貢獻而命名的。
非國際單位制單位包括爾格、英尺·磅、千瓦小時（kW·h）、大氣壓力、馬力小時（HP·h）。而由於具有相同的物理量─熱能，偶爾會見到以熱量熱能形式表示的測量單位，如：卡路里（cal）、BTU等。

內容

功等於力與物體在力的方向上通過距離的乘積。
對於一移動的物體而言，作功量/時間可以從距離/時間（即速度V）來計算。因此，在任何時刻，力所作的功率（焦耳/秒、瓦），其值為力的標量積（矢量）和作用點上的速度矢量。力的標量積和速度被歸類為瞬時功率。
而正如速度可能會隨著時間的推移以獲得更長的距離，同一條路徑上的總功率也同樣是作用點沿著同一條路徑上之瞬時功率的時間積分的總和。
功是指質點受外力作用位移而產生的量，當質點移動時，它沿著曲線X和速度V在所有的時間t。少量的功δW發生在瞬時時間δt能夠寫成：
  • 其中F.v是在δt內的瞬時功率，這些少量功的總合超過該質點運動位移所產生的功量。
    其中C的位移是從x（t1） 到x（t2），計算質點位移的積分。
    如果力的方向總是沿著這條線，力的大小為F，那么此積分可簡化為:
      其中s是沿著直線的位移，假設F固定，且沿著此直線，則此積分可進一步簡化成：
        其中d是質點沿著直線前進的距離。
        此計算可歸納為恆定力並非延著線而是沿著質點。在此情況下點的乘積F·dx=Fcosθdx，其中θ是力矢量和運動方向之間的角度。即：
          一般常見的情況，施加的力和速度矢量對身體成90角（中央力朝下身體繞一圓圈運動），由於cos90為0，所以不作功。因此可以延伸至重力對於星球在圓形軌道上運動不作功（此為理想情況，一般情況下軌道略呈橢圓形）。
          此外身體作一等速圓周運動受到機械外力作用時，作的功也為0，就像在一理想情況之無摩擦力的離心機中作等速圓周運動一般。
          計算功在時間和力作用在一直線路徑上的數值只適用在最簡單的情況下，如上文所述。如果力會變化，或身體延曲線方向移動，物體可能轉動甚至並非剛性物體，那么其所作的功只和作用力的角度、路徑有關，並且只有部分的力平行在作用點上形成的速度才作功 （相同方向為正，反方向為負值），此處的力可以被描述為標量或是切線分量的標量。（Fcosθ，其中θ是力和速度之間的夾角）。
          至於功最普遍的定義如下：力所的功是其延著作用點上的路徑之切線分量的標量也就是線性積分。

          轉矩和轉動

          轉矩是從相等但方向相反的力作用於剛性體上兩個不同的點所形成。這些力總合為零，但它會對物體影響形成轉矩Τ，計算作功形成的轉矩公式為：
          • ，其中T.ω是作用在時間點δt上。這些少量的功之合大於剛性體運動軌跡所產生的功。
          • ，此積分是計算剛體延軌跡運動與時間變化的角速度ω，可以說與運動的路徑息息相關。
          如果角速度矢量保持恆定的方向，那么可以寫成：
          • ，其中φ為轉動角度，單位矢量S。在此情況下，功的轉矩可寫成：
          • ，其中C是從φ（t1）到φ（t2）的運動軌跡。此積分取決於φ（t）的值，因此與路徑相關。
          如果轉矩T與角速度矢量一致，那么可寫成：
            而且若轉矩和角速度是恆定的，那么功可寫成這個形式：
              A force of constant magnitude and perpendicular to the lever arm
              此結果可以更簡單的理解，如圖所示。這股力將通過圓弧的距離s=rφ，所作的功即是：
              • ，導出轉矩τ=Fr，得：
              以上，請注意只有轉矩在角速度矢量方向的部分才有作功。

              力與位移

              力與位移都是矢量。功是力與位移的內積，為標量。
              • （1）
              其中是力矢量和位移矢量的夾角。
              為使此式正確，力須為常矢量，路徑須為一條直線。
              如力隨時間變化或路徑不為直線，上式不再適用，此時需使用曲線積分。故功的一般公式為：
              • （2）
              其中
              • 是路徑；
              • 是力矢量；
              • 是位移矢量。
              表達式是一個非恰當微分，與路徑有關，求微分後不能得到。
              非零力可以不做功，這一點與衝量不同。衝量是力對時間的累積。衝量是矢量，所以圓周運動時雖向心力不做功，但產生了對物體的非零衝量。

              力矩

              力矩所做功可由下式計算得到：
                其中為力矩。

                力與位移

                力與位移都是矢量。功是力與位移的內積，為標量。
                (1) 其中θ是力矢量和位移矢量的夾角。
                為使此式正確，力須為常矢量，路徑須為一條直線。
                如力隨時間變化或路徑不為直線，上式不再適用，此時需使用線積分。故功的一般公式為：
                功(力和力在力的方向上通過位移的乘積)
                (2) 其中 C是路徑；
                是力矢量；
                是位移矢量。 表達式是一個非恰當微分，與路徑有關，求微分後不能得到
                。
                非零力可以不做功，這一點與衝量不同。衝量是力對時間的累積。衝量是矢量，所以圓周運動時雖向心力不做功，但產生了對物體的非零衝量。
                力矩所做功可由下式計算得到：
                其中為力矩。

                比較做功的快慢

                方法一：
                做功相同，比時間。時間越短，做功越快。
                方法二：
                時間相同，比做功。做功越多，做功越快。
                方法三：
                做功和時間均不相同，比比值。
                做功/時間的值越大，做功越快。

                與能的關係

                一個物體對外做了多少功，它就減少了多少能量。反之，外界對一個物體做了多少功，這個物體的能量就增加了多少。（功與能單位相同）

                內容

                常力的功

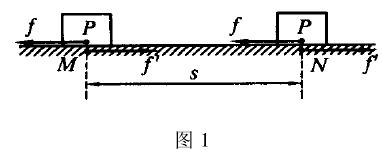
                大小和方向都不變的力F，作用於沿直線運動的物體上（圖1），力作用點的位移為S，則力F對
                功(力和力在力的方向上通過位移的乘積)
                該物體所作的功A為，
                功(力和力在力的方向上通過位移的乘積)
                式中α為F和S的夾角。當α<
                時，功為正值：當α>
                時，功為負值；當α=
                時，即力和位移方向垂直，力在此位移上不作功。

                變力的功

                大小和方向變化的力F，作用於沿曲線運動物體的C點上（圖2）。當作用點有微小的位移dr時（|dr|=dS），在其上的力F可視為不變，因此，力F在微小位移dS上所作的元功為：
                功(力和力在力的方向上通過位移的乘積)
                dA=F cos α dS=F·dr=Fxdx+Fvdy+Fzdz。
                將整個路程上力在各微段的元功總和起來，得力F沿曲線ab的總功：
                功(力和力在力的方向上通過位移的乘積)
                式中a、b為曲線運動的起止點。知道變力F隨路程S的變化關係，就可由上式求出功的量值。
                物體作曲線運動時，法向力Fn與位移垂直不做功，故總功只與切向力Fi有關，即A=
                功(力和力在力的方向上通過位移的乘積)
                合力的功 如有m個力F1，F2，···，Fm作用於物體的一點上，則這些力的功為：
                功(力和力在力的方向上通過位移的乘積)
                式中R=
                為諸力的合力，Ri為合力的切向分量。

                力偶的功

                力偶的功可表示為：
                功(力和力在力的方向上通過位移的乘積)
                式中T為作用於剛體上的力偶矩；ω為剛體的角速度；t為時間。當剛體作平動時，ω=0，則力偶之功為零。當剛體作平面一般運動時，T和ω均可看作代數量，故有：
                功(力和力在力的方向上通過位移的乘積)
                T和ω轉向相同時，取正號；相反時，取負號。

                參考文獻

                1、詞條作者：戴宗信．《中國大百科全書》74卷（第一版）力學 詞條：功：中國大百科全書出版社，1987 ：182頁

                相關詞條

                熱門詞條

                聯絡我們