基本介紹
- 中文名:單位矩陣
- 外文名:identity matrix
- 學科:數理科學
- 類型:方陣
- 特點:主對角線上的元素都為1
- 表示:I或E
- 適用範圍:線性代數
- 特性:AI=IA=A
矩陣
簡介


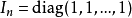
性質
單位矩陣在高等代數中的套用
求等價標準型問題

求逆矩陣問題




matlab 生成單位矩陣的方法





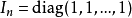







在矩陣的乘法中,有一種矩陣起著特殊的作用,如同數的乘法中的1,這種矩陣被稱為單位矩陣。它是個方陣,從左上角到右下角的對角線(稱為主對角線)上的元素均為1...
矩陣單位,即單位矩陣。線上性代數中,n階單位矩陣,是一個n*n的方形矩陣,其主對角線元素為1,其餘元素為0。...
單位陣是單位矩陣的簡稱,它指的是主對角線上都是1,其餘元素皆為0的矩陣。...... 單位陣是單位矩陣的簡稱,它指的是主對角線上都是1,其餘元素皆為0的矩陣。...
零矩陣,在數學中,特別是線上性代數中,零矩陣即所有元素皆為0的矩陣。在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及...
矩陣相乘最重要的方法是一般矩陣乘積。它只有在第一個矩陣的列數(column)和第二個矩陣的行數(row)相同時才有意義。一般單指矩陣乘積時,指的便是一般矩陣乘積。...
矩陣的秩是線性代數中的一個概念。線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數。通常表示為r(A),rk(A)或rank A。線上性代數中,一個矩陣A...
初等矩陣是指由單位矩陣經過一次三種矩陣初等變換得到的矩陣。初等矩陣的模樣可以寫一個3階或者4階的單位矩陣。首先:初等矩陣都可逆,其次,初等矩陣的逆矩陣其實是一...
設A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,則稱 m 是矩陣A的一個特徵值(characteristic value)或本徵值(eigenvalue)。...
設A是n階矩陣, 若r(A) = n, 則稱A為滿秩矩陣。但滿秩不局限於n階矩陣。若矩陣秩等於行數,稱為行滿秩;若矩陣秩等於列數,稱為列滿秩。既是行滿秩又...
GE矩陣(GE Matrix/Mckinsey Matrix) GE矩陣法又稱通用電氣公司法、麥肯錫矩陣、九盒矩陣法、行業吸引力矩陣。在戰略規划過程中,套用GE矩陣必須經歷以下5個步驟,GE...
單位元素是集合里的一種特別的元素,與該集合里的二元運算有關。當單位元和其他元素結合時,並不會改變那些元素。單位元被使用在群和其他相關概念之中。...
生成矩陣是線性碼的一種表示。e元[n,a]線性碼C的一個生成矩陣是有限域Fₑ上的一個a×n矩陣,其行向量構成子空間C的一組基,設C與C′是兩個e元線性碼,G...
M矩陣是L矩陣的一種,M矩陣要求它自身的逆矩陣為一個非負矩陣。...... (9) B=λI-A為非負矩陣,其中I為單位矩陣,λ>ρ(B)。(10) 若B為L矩陣,且bij>=...
單位元(英文常寫作Identity Element,即IE)是集合里的一種特別的元,與該集合里的運算(可理解為實數里的*,但並不局限於)有關。當它和其他元素結合時,並不會...
