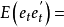VAR(計算機術語):術語介紹,金融術語,基本思想,基本模型,假設條件,模型套用,

計算機語言中的var：Pascal: var 在Pascal 作為程式的保留字，用於定義變數。如：var a:integer；（定義變數a，類型為整數） var u:array[1..100]of integer；（定義數組u，下標由1至100，數組單元類型為整數）

基本介紹

中文名：var
外文名：var
概述：計算機語言中的var：Pascal
術語介紹：var 是 variable（變數）
作用：用於定義變數

術語介紹,金融術語,基本思想,基本模型,假設條件,模型套用,計量風險,分析結論,物理單位,相關信息,機率術語,向量自回歸,音樂術語,增值經銷商,

術語介紹

var 是 variable（變數，可變物）或者是variation的簡寫。在多種計算機程式語言中，var 被用作定義變數的關鍵字，在一些作業系統中也能見到它的身影。

Swift

在Swift 中var 也用來定義變數。

JavaScript

var a=10; //正確

a=10; //正確

在javascript中，以上兩種方法都是定義變數的正確方法。微軟的Script56.CHM中是這樣解釋的：

儘管並不安全，但聲明語句中忽略var關鍵字是合法的 JScript 語法。這時，JScript 解釋器給予變數全局範圍的可見度。當在過程級中聲明一個變數時，它不能用於全局範圍；這種情況下，變數聲明必須用var關鍵字。

從上面的描述看來，對待這兩種定義方法要區分以下兩種情況：

⒈在一個過程級中（即位於function的定義範圍內，無論是函式，還是類）的任何地方，包括在一個區塊里（for,while,if……），定義變數時，使用var定義，則此變數只在這個過程級內起作用，反之為全局變數。

⒉在過程級外定義變數時，無論是否忽略var，都將定義一個全局變數。

從這點看來，JS和其他語言有不一樣的地方，變數的範圍不以“{}”作為邊界，而是以"function(){}"為邊界，而且在過程內可以很輕鬆的定義全局變數。如果不注意這個問題的話，是很容易產生不可預知的錯誤的。

對於使用var，我的建議是要養成好的使用習慣：

⒈在程式的開頭，統一定義全局變數；

⒉所有的變數在定義時都要加上var；

⒊儘量不要在不同的過程中使用相同的變數名。

Pascal

VAR 在Pascal 作為程式的保留字，用於定義變數。如：

var a:integer; （定義變數a，類型為整數）

var u:array[1..100]of integer；（定義數組u，下標由1至100，數組單元類型為整數）

常用變數類型（具體見變數詞條）：

integer 整型

longint 長整型

real 實數型

char 字元型

string 字元串

array 數組

……

當同時定義多個變數時，只需使用一次var，相同類型的變數也可以寫在一起。

var a,b,c:integer;

s,t:longint;

ch1,ch2:char;

st:string;

data:array[1..255]of real;

當然了，並不是所有程式語言中都需要var來定義變數，比如說C語言、JAVA語言都不需要利用VAR來定義變數而是直接寫即可，比如：int a=0;

從 Visual C# 3.0 開始，在方法範圍中聲明的變數可以具有隱式類型VAR。隱式類型的本地變數是強類型變數，但由編譯器確定類型。

VAR可代替任何類型

編譯器會根據上下文來判斷你到底是想用什麼類型的

什麼情況下用到VAR：

當你無法確定自己將用的是什麼類型，就可以使用VAR

類似OBJECT，但是效率比OBJECT高點

ASP

同c#，弱類型的定義變數。

VAR可代替任何類型

編譯器會根據上下文來判斷你到底是想用什麼類型的

什麼情況下用到VAR：

當你無法確定自己將用的是什麼類型，就可以使用VAR

類似OBJECT，但是效率比OBJECT高點

使用var定義變數時有以下四個特點：

⒈ 必須在定義時初始化。也就是必須是var s = “abcd”形式，而不能是如下形式：

var s;

s = “abcd”；

⒉ 一但初始化完成，就不能再給變數賦與初始化值類型不同的值了。

⒊ var要求是局部變數。

⒋ 使用var定義變數和object不同，它在效率上和使用強類型方式定義變數完全一樣。

ASP中，我們可以利用var進行檢索，如

Dim a⑵

a(0)=0

a⑴=0

a⑵=0

var可以進行檢索

var0=a(0)

var1=a⑴

var1=a⑵

在C#和ASP中，使用var定義變數時有以下四個特點：

⒈ 必須在定義時初始化。也就是必須是var s = “abcd”形式，而不能是如下形式：

var s;

s = “abcd”；

⒉ 一但初始化完成，就不能再給變數賦與初始化值類型不同的值了。

⒊ var要求是局部變數。

⒋ 使用var定義變數和object不同，它在效率上和使用強類型方式定義變數完全一樣。

Linux

/var 目錄，包括系統運行時要改變的數據。其中包括每個系統是特定的，即不能夠與其他計算機共享的目錄，如/var/log，/var/lock，/var/run。有些目錄還是可以與其他系統共享，如/var/mail,/var/cache/man,/var/cache/fonts,/var/spool/news。var目錄存在的目的是把usr目錄在運行過程中需要更改的檔案或者臨時生成的檔案及目錄提取出來，由此可以使usr目錄掛載為唯讀的方式。linux的命令都是基於shell的，可以選擇不同的shell類型。

HTML

在HTML中，<var> 標籤表示數學表達式或編程上下文中的變數，<var> 標籤定義的內容會呈現為斜體。

使用方法：

<var>變數</var>

全局屬性：

accesskey、class、data-*、dir、lang、spellcheck、style、tabindex、draggable、contenteditable、translate、title

金融術語

VaR（Value at Risk）一般被稱為“風險價值”或“在險價值”，指在一定的置信水平下，某一金融資產（或證券組合）在未來特定的一段時間內的最大可能損失。假定JP摩根公司在2004年置信水平為95%的日VaR值為960萬美元，其含義指該公司可以以95%的把握保證，2004年某一特定時點上的金融資產在未來24小時內，由於市場價格變動帶來的損失不會超過960萬美元。或者說，只有5%的可能損失超過960萬美元。與傳統風險度量手段不同，VaR完全是基於統計分析基礎上的風險度量技術，它的產生是JP摩根公司用來計算市場風險的產物。但是，VaR的分析方法正在逐步被引入信用風險管理領域。

基本思想

VaR按字面的解釋就是“處於風險狀態的價值”，即在一定置信水平和一定持有期內，某一金融工具或其組合在未來資產價格波動下所面臨的最大損失額。JP.Morgan定義為：VaR是在既定頭寸被沖銷（be neutraliged）或重估前可能發生的市場價值最大損失的估計值；而Jorion則把VaR定義為：“給定置信區間的一個持有期內的最壞的預期損失”。

基本模型

根據Jorion(1996），VaR可定義為：

VaR=E（ω）-ω* ①

式中E（ω）為資產組合的預期價值；ω為資產組合的期末價值；ω*為置信水平α下投資組合的最低期末價值。

又設ω=ω0(1+R） ②

式中ω0為持有期初資產組合價值，R為設定持有期內（通常一年）資產組合的收益率。

ω*=ω0(1+R*） ③

R*為資產組合在置信水平α下的最低收益率。

根據數學期望值的基本性質，將②、③式代入①式，有

VaR=E[ω0(1+R）]-ω0(1+R*）

=Eω0+Eω0（R）-ω0-ω0R*

=ω0+ω0E（R）-ω0-ω0R*

=ω0E（R）-ω0R*

=ω0[E（R）-R*]

∴VaR=ω0[E（R）-R*] ④

上式公式中④即為該資產組合的VaR值，根據公式④，如果能求出置信水平α下的R*，即可求出該資產組合的VaR值。

假設條件

VaR模型通常假設如下：

⒈市場有效性假設；

⒉市場波動是隨機的，不存在自相關。

一般來說，利用數學模型定量分析社會經濟現象，都必須遵循其假設條件，特別是對於中國金融業來說，由於市場尚需規範，政府干預行為較為嚴重，不能完全滿足強有效性和市場波動的隨機性，在利用VaR模型時，只能近似地正態處理。

VaR模型計算方法

從前面①、④兩式可看出，計算VAR相當於計算E（ω）和ω*或者E（R）和R*的數值。從目前來看，主要採用三種方法計算VaR值。

⒈歷史模擬法（historical simulation method）

⒉方差—協方差法

⒊蒙特卡羅模擬法（Monte Carlo simulation）

三種方法的異同點的比較:

	Variance	Monte Carlo	Historical
Portfolio Valuation	Delta approximation (linear)	Full/Approximation	Full
Assumed Distribution of Returns	Normal distributuon	Flexible(usually the normal distribution)	Actual
Requirement for Cashflow Mapping	Yes	No	No
Suitability for options	No(unless holding period si short adn portfolio has moderate options content)	Yes	Yes
Computation and implementation	Relatively easy to compute and implement	Can be costly and show depending on the number of simulation runs required	Easy to compute and implement
Accuracy of VAR Estimate	Depends on vailidity of normality assumption and degree of portfolio optionality	Generally the most reliable method provided sufficient simulation runs are carried out	Good,provided the historical data is a relibale data is a reliable guide to future market behavior

一．歷史模擬法

“歷史模擬法”是藉助於計算過去一段時間內的資產組合風險收益的頻度分布，通過找到歷史上一段時間內的平均收益，以及在既定置信水平α下的最低收益率，計算資產組合的VaR值。

“歷史模擬法”假定收益隨時間獨立同分布，以收益的歷史數據樣本的直方圖作為對收益真實分布的估計，分布形式完全由數據決定，不會丟失和扭曲信息，然後用歷史數據樣本直方圖的P—分位數據作為對收益分布的P—分位數—波動的估計。

一般地，在頻度分布圖中（圖1，見例1）橫軸衡量某機構某日收入的大小，縱軸衡量一年內出現相應收入組的天數，以此反映該機構過去一年內資產組合收益的頻度分布。

首先，計算平均每日收入E（ω）

其次，確定ω*的大小，相當於圖中左端每日收入為負數的區間內，給定置信水平α，尋找和確定相應最低的每日收益值。

設定信水平為α，由於觀測日為T，則意味差在圖的左端讓出

t=T×α，即可得到α機率水平下的最低值ω*。由此可得：

VaR=E（ω）-ω*

二.方差—協方差法

“方差—協方差”法同樣是運用歷史資料，計算資產組合的VaR值。其基本思路為：

首先，利用歷史數據計算資產組合的收益的方差、標準差、協方差；

其次，假定資產組合收益是常態分配，可求出在一定置信水平下，反映了分布偏離均值程度的臨界值；

第三，建立與風險損失的聯繫，推導VaR值。

設某一資產組合在單位時間內的均值為μ，標準差為σ，R*～μ（μ、σ），又設α為置信水平α下的臨界值，根據常態分配的性質，在α機率水平下，可能發生的偏離均值的最大距離為μ-ασ，

即R*=μ-ασ。

∵E（R）=μ

根據VaR=ω0[E（R）-R*] 有

VaR=ω0[μ-（μ-ασ）]=ω0ασ

假設持有期為 △t，則均值和數準差分別為μ△t和，這時上式則變為：

VaR=ω0·α·

因此，我們只要能計算出某種組合的數準差σ，則可求出其VaR的值，一般情況下，某種組合的數準差σ可通過如下公式來計算

其中，n為資產組合的金融工具種類，Pi為第i種金融工具的市場價值，σi第i種金融工具的數準差，σij為金融工具i、j的相關係數。

三、蒙特卡羅模擬法（Monte Carlo simulation）

除了歷史模擬法和方差—數準差法外，對於計算資產組合的VaR的方法還有更為複雜的“蒙特卡羅模擬法”。它是基於歷史數據和既定分布假定的參數特徵，藉助隨機產生的方法模擬出大量的資產組合收益的數值，再計算VaR值。

⒈確認頭寸找到受市場風險影響的各種金融工具的全部頭寸

⒉確認風險因素確認影響資產組合中金融工具的各種風險因素

⒊獲得持有期內風險因素的收益分布計算以往年份里的歷史上的頻度分布計算以往年份里風險因素的標準差和相關係數假定特定的參數分布或從歷史資料中按自助法隨機產生

⒋將風險因素的收益與金融工具頭寸相聯繫將頭寸的盯住市場價值（mark to market value）表示為風險因素的函式按照風險因素分解頭寸（risk mapping）將頭寸的盯住市場價值（mark to market value）表示為風險因素的函式

⒌計算資產組合的可變性利用從步驟3和步驟4得到的結果模擬資產組合收益的頻度分布假定風險因素是呈常態分配，計算資產組合的標準差利用從步驟3和步驟4得到的結果模擬資產組合收益的頻度分布

⒍給定置信區間推導VAR

排列資產組合順序，選擇剛好在1%或5%機率下剛≥1的那一損失

用2.33(1%）或1.65(5%）乘以資產組合標準差排列資產組合順序，選擇剛好在1%或5%機率下剛≥1的那一損失

模型套用

VaR模型在金融風險管理中的套用越來越廣泛，特別是隨著VaR模型的不斷改進，不但套用於金融機構的市場風險、使用風險的定量研究，而且VaR模型正與線性規劃模型（LPM）和非線性規劃模型（ULPM）等規劃模型論，有機地結合起來，確定金融機構市場風險等的最佳定量分析法，以利於金融機構對於潛在風險控制進行最優決策。

對於VaR在國外的套用，正如文中引言指出，巴塞爾委員會要求有條件的銀行將VaR值結合銀行內部模型，計算適應市場風險要求的資本數額；G20建議用VaR來衡量衍生工具的市場風險，並且認為是市場風險測量和控制的最佳方法；SEC也要求美國公司採用VaR模型作為三種可行的披露其衍生交易活動信息的方法之一。這表明不但金融機構內部越來越多地採用VaR作為評判金融機構本身的金融風險，同時，越來越多的督管機構也用VaR方法作為評判金融機構風險大小的方法。

中國對VaR模型的引介始於近年，具有較多的研究成果，但VaR模型的套用正確處於起步階段，各金融機構已經充分認識到VaR的優點，正在研究適合於自身經營特點的VaR模型。

本部分就VAR模型在金融機構風險管理中的套用及其注意的問題介紹如下：

例1，來自JP.Morgan的例子

根據JP.Morgan1994年年報披露，該公司1994年一天的95%VAR值平均為1500萬美元，這一結果可從反映JP.Morgan1994年日收益分布狀況圖中求出（如圖）。

從圖中可看出，該公司日均收益為500萬美元，即E（ω）=500萬美元。

如果給定α=95%，只需找一個ω*，使日收益率低於ω*的機率為5%，或者使日收益率低於ω*的ω出現的天數為254×5%=13天，從圖中可以看出，ω*=－1000萬美元。

根據VAR=E（ω）－ω*=500－（－1000）=1500萬美元

值得注意的是，這只是過去一段時間的數值，依據過去推測未來的準確性取決於決定歷史結果的各種因素、條件和形勢等，以及這些因素是否具有同質性，否則，就要做出相應的調查，或者對歷史數據進行修正。這在中國由於金融機構非完全市場作用得到的數據更應該引起重視。

例2，來自長城證券杜海濤的研究

長城證券公司杜海濤在《VaR模型在證券風險管理中的套用》一文中，用VaR模型研究了市場指數的風險度量、單個證券的風險度量和證券投資基金淨值的VaR等，研究表明，VaR模型對中國證券市場上的風險管理有較好的效果。

下面就作者關於市場指數的風險度量過程作一引用，旨在說明VaR的計算過程（本文引用時有刪節）。

第一步正態性檢驗

首先根據2000年1月4日至2000年6月2日期間共94個交易日的日收益率做分布直方圖，由於深滬兩市場具有高度相關性，此處僅以上證綜合指數為例計算。結果如圖1。

從圖1可以看出上證綜合指數日收益率分布表現出較強的正態特徵：眾數附近十分集中，尾部細小。分析表明，深市指數也有相同的特徵。

下面利用數理統計的方法對2000年4月3日至6月2日期間上述3種指數的日收益率的分布情況進行正態性檢驗，檢驗結果如下：

W（深證綜指）=0.972445

W（深證成指）=0.978764

W（上證綜指）=0.970279

W為正態假設檢驗統計量，當樣本容量為40時取α =0.05（表示我們犯錯誤的機率僅為 α=0.05），此時W0.05 =0.94，只有當W <W0.05 時我們拒絕原假設。從我們的檢驗結果來看，我們無法拒絕三種指數的日收益率服從常態分配的假設。

有關這三種指數日收益率的相關統計量見表1。

表1 三種指數日收益率統計量

深圳綜合深圳成分上證綜合

均值（）

0.001318 0.001061 0.001561

標準差（）

0.013363 0.012582 0.012391

通過上面的分析，我們可以得出三種指數的日收益率基本上服從N（μ，σ），由於三種指數的平均日收益率非常接近零值，故可近似為N(0，σ）。

第二步 VaR的計算

由於常態分配的特點，集中在均值附近左右各1.65σ區間範圍內的機率為0.90，用公式表示為：P（μ-1.65σ<X<；μ+1.65σ）=0.90，再根據常態分配的對稱性可知P(X<；μ-1.65σ）=P(X>；μ+1.65σ）=0.05；則有P(X>；μ-1.65σ）=0.95。根據上面的計算結果可知在95%的置信度情況下：

VaR值=T日的收盤價×1.65σ。

取2000年4月3日至2000年6月2日的數據，然後根據上面的公式可以計算出深證綜指、深證成指、上證綜指3種指數在2000年6月2日的VaR值分別為：

深證綜合指數VaR=591.34×1.65×0.013363=13.04

深證成份指數VaR=4728.88×1.65×0.012582=98.17

上證綜合指數VaR=1916.25×1.65×0.012391=39.17

其現實意義為：根據該模型可以有95%的把握判斷指數在下一交易日即6月5日的收盤價不會低於T日收盤價－當日的VaR值；

即深證綜合指數不會低於：591.34－13.04=578.30

深證成份指數不會低於：4728.88－98.17=4630.71

上證綜合指數不會低於：1916.25－39.17=1877.08。

第三步可靠性檢驗

接著來檢驗該模型的可靠性。根據3種指數的VaR來預測下一個交易日的指數變動下限，並比較該下限和實際收盤價，看預測的結果與我們期望值之間的差別。圖2、圖3、圖4是3個指數於2000年4月3日至6月2日的實際走勢與利用VaR預期下限的擬合圖形。

現將樣本區間內實際收盤指數低於預測下限的天數與95%置信度情況下的可能出現的期望天數作一統計對比，結果見表2。

表2 模型期望結果與實際結果的比較

深圳綜合深圳成分上證綜合

實際情況 3 3 3

期望情況 2 2 2

通過上面的計算我們可以發現套用VaR模型進行指數風險控制擬合結果較好。至於三種指數均有3個交易日超過預測下限，這主要是由於考察期間適逢台灣政權更迭及美眾院審議表決予華PNTR的議案，市場波動較大所致。

例3，來自銀行家信託公司的例子

由於金融機構特別是在證券投資中，高收益常伴隨著高風險，下級部門或者交易員可能冒巨大風險追求利潤，但金融機構出於穩健經營的需要，有必要對下級部門或者交易員可能的過渡投資機行為進行限制，因而引入考慮風險因素的業績評價體系，美國銀行和信託公司將VaR模型用於業績評估中，確立了業績評價指數——經風險調查的資本收益，即RAROC= ，從公式可看出，即使收益再高，但由於VaR也高，則RAROC也不會很高，其業績評價也不可能很高。因此，將金融機構將VaR套用於業績評價中，可對過度投機行為進行限制，使金融機構能更好地選擇在最小風險下獲取較大收益的項目。

同時，杜海濤也將VaR方法用於對中國5隻基金管理人的經營業績評價，評價結果如下表：

中國5隻基金管理人的RAROC比較表

基金開元基金普惠基金金泰基金安信基金裕陽

VaR值 0.1178 0.0919 0.0880 0.1240 0.1185

收益率0.4153 0.2982 0.3592 0.4206 0.3309

RAROC 2.8467 2.7495 3.5188 3.1707 2.7938

日收益率的標準差 0.045623 0.03748 0.035623 0.037033 0.036559

數據來源：杜海濤《VaR模型在證券風險管理中的套用》

從上表可以看出，在承擔同樣的風險的情況下基金金泰的收益率最高。按RAROC指標來衡量上述5家證券投資基金的優劣情況如下：金泰>；安信>；開元>；裕陽>；普惠。

計量風險

在風險管理的各種方法中，在險價值法（VAR方法）最為引人矚目。尤其是在過去的幾年裡，許多銀行和監管當局開始把這種方法當作全行業衡量風險的一種標準來看待。

一在險價值（VaR）的計算

在險價值法之所以具有吸引力，是因為它把銀行的全部資產組合風險概括為一個簡單的數字，並以美元計量單位來表示風險管理的核心-潛在虧損。VaR實際上是要回答在機率給定的情況下，銀行的投資組合價值在下一階段最多可能損失多少。在常態分配情況下，根據計量經濟學的知識可得出：

VaR =w0ua d t1/2

其中，w0 為初期投資額，m 和d2分別為特定資產的日（或者周、年）回報率的均值和方差，d則代表資產回報率的標準差，t為持有該項資產的期間。

此公式的含義是：在特定資產回酬率R服從常態分配的情況下，一定投資額w0在置信度1-a的範圍內，在持有時間t內發生的最大損失。

如要求置信度為95%或99%，即a=5%或1%，應該查相對應的10%和2%的常態分配表，相應公式可變為：VaR =1.645 w0dt1/2或者 VaR =2.33 w0dt1/2

由此可見，為了計算VaR的數值，首先必須估算出資產回報率的均值和標準差，目前一般是通過對觀察值進行加權來計算出來的。

實例如下：假定有一3年期100萬美元國債券，假定過去10年此類債券價格的平均波動率為1.23%，如果此種國庫券半年後出售，價格波動服從常態分配，並確定為95%的置信水平，則有：

VaR =100×1.645×1.23%×0.51/2 = 1.44（萬美元）

這表明，依據歷史統計資料，我們至少有95%的把握可以保證3年期國庫券價格在以後6個月出售，最大損失不超過1.44萬美元。由於是單邊機率，我們還可得出結論：依據歷史統計資料，至少有95%的把握可以保證3年期國庫券價格在以後6個月出售，最大盈利不會超過1.44萬美元。

二在險價值法的特點

⒈可以用來簡單明了地表示市場風險的大小，單位是美元或其他貨幣，沒有任何技術色彩，沒有任何專業背景的投資者和管理者都可以通過VaR值對金融風險進行評判；

⒉可以事前計算風險，不像以往風險管理的方法都是在事後衡量風險大小；

⒊不僅能計算單個金融工具的風險，還能計算由多個金融工具組成的投資組合的風險，這是傳統金融風險管理所不能做到的。

三在險價值法的套用

該方法主要套用於：

⒈ 用於風險控制。

目前已有超過1000家的銀行、保險公司、投資基金、養老金基金及非金融公司，採用VaR方法作為金融衍生工具風險管理的手段。利用VAR方法進行風險控制，可以使每個交易員或交易單位都能確切地明了他們在進行有多大風險的金融交易，並可以為每個交易員或交易單位設定VAR限額，以防止過度投機行為的出現。如果執行嚴格的VaR管理，一些金融交易的重大虧損也許就完全可以避免。

⒉ 用於業績評估。

在金融投資中，高收益總是伴隨著高風險，交易員可能不惜冒巨大的風險去追逐巨額利率。公司出於穩健經營的需要，必須對交易員可能的過度投機行為進行限制。所以，有必要引入考慮風險因素的業績評價指標。

四在險價值法的局限

當然VaR方法也有其局限性，VaR方法衡量的主要是市場風險，如單純依靠VaR方法，就會忽視其他種類的風險如信用風險。另外，從技術角度講，VaR值表明的是一定置信度內的最大損失，但並不能絕對排除高於VaR值的損失發生的可能性。例如假設一天的99%置信度下的VaR=1000萬美元，仍會有1%的可能性會使損失超過1000萬美元。這種情況一旦發生，給經營單位帶來的後果就是災難性的。所以在金融風險管理中，VaR方法並不能涵蓋一切，仍需綜合使用各種其他的定性、定量分析方法。亞洲金融危機還提醒風險管理者：在險價值法並不能預測到投資組合的確切損失程度，也無法捕捉到市場風險與信用風險間的相互關係。

分析結論

隨著中國加入WTO，金融全球化挑戰中國的金融改革及創新，特別是金融理論的創新和控制風險技術的創新，如何將金融風險控制到最小程度，真正使金融體系成為支撐社會經濟的基礎，達到為社會分散經濟風險的目的，是中國金融界必須面對的艱巨任務，如何用定量方法測度和控制金融風險，是金融機構和監管當局必須面對的問題。從金融機構本身來看，將風險定量分析方法，比如VaR模型套用於日常的風險管理，將市場風險和信用風險降到最低的程度，以期獲取最大的利潤回報，是金融機構的義不容辭的事情，也是其當務之急。從監管當局來看，促使金融機構套用先進的控制風險技術，使金融家們能夠隨心所欲地剝離各種風險，即對各種複雜的風險進行精確的計算和配置，將有利於中國的監管水平有較大的提高。因此，中國的金融機構和金融監管當局非常有必要將VaR模型等風險控制技術引入中國金融風險管理將非常必要，且具有一定的現實意義。

物理單位

Var （乏）或 Vars 或 kVar（千乏）是交流電路中無功功率的單位，其大小與有功功率的單位Watts是相同的，

無功功率

在交流電路中，由電源供給負載的電功率有兩種；一種是有功功率，一種是無功功率。

有功功率是保持用電設備正常運行所需的電功率，也就是將電能轉換為其他形式能量（機械能、光能、熱能）的電功率。比如：5.5千瓦的電動機就是把5.5千瓦的電能轉換為機械能，帶動水泵抽水或脫粒機脫粒；各種照明設備將電能轉換為光能，供人們生活和工作照明。有功功率的符號用P表示，單位有瓦（W）、千瓦（kW）、兆瓦（MW）。

無功功率比較抽象，它是用於電路內電場與磁場的交換，並用來在電氣設備中建立和維持磁場的電功率。它不對外作功，而是轉變為其他形式的能量。凡是有電磁線圈的電氣設備，要建立磁場，就要消耗無功功率。比如40瓦的日光燈，除需40多瓦有功功率（鎮流器也需消耗一部分有功功率）來發光外，還需80乏左右的無功功率供鎮流器的線圈建立交變磁場用。由於它不對外做功，才被稱之為“無功”。無功功率的符號用Q表示，單位為乏（Var）或千乏（kVar）。

無功功率決不是無用功率，它的用處很大。電動機需要建立和維持旋轉磁場，使轉子轉動，從而帶動機械運動，電動機的轉子磁場就是靠從電源取得無功功率建立的。變壓器也同樣需要無功功率，才能使變壓器的一次線圈產生磁場，在二次線圈感應出電壓。因此，沒有無功功率，電動機就不會轉動，變壓器也不能變壓，交流接觸器不會吸合。為了形象地說明這個問題，現舉一個例子：農村修水利需要開挖土方運土，運土時用竹筐裝滿土，挑走的土好比是有功功率，挑空竹筐就好比是無功功率，竹筐並不是沒用，沒有竹筐泥土怎么運到堤上呢?

在正常情況下，用電設備不但要從電源取得有功功率，同時還需要從電源取得無功功率。如果電網中的無功功率供不應求，用電設備就沒有足夠的無功功率來建立正常的電磁場，那么，這些用電設備就不能維持在額定情況下工作，用電設備的端電壓就要下降，從而影響用電設備的正常運行。

無功功率對供、用電產生一定的不良影響，主要表現如下：

⑴降低發電機有功功率的輸出。

⑵降低輸、變電設備的供電能力。

⑶造成線路電壓損失增大和電能損耗的增加。

⑷造成低功率因數運行和電壓下降，使電氣設備容量得不到充分發揮。

從發電機和高壓輸電線供給的無功功率，遠遠滿足不了負荷的需要，所以在電網中要設定一些無功補償裝置來補充無功功率，以保證用戶對無功功率的需要，這樣用電設備才能在額定電壓下工作。這就是電網需要裝設無功補償裝置的道理。

kVar：無功功率的單位千乏。電功率分為有功功率和無功功率，有功功率就是指電能轉化為熱能或者機械能等形式被人們使用或消耗的能量；無功功率指電場能和磁場能相互轉化的那部分能量，它的存在使電流與電壓產生相位偏差，為了區別於有功功率就用了這么個單位。

電網中由於有大功率電機的存在，使得其總體呈感性，所以常常在電網中引入大功率無功補償器（其實就是大電容），使電網近似於純阻性，kVar就常用在這作為無功補償器的容量的單位，跟千瓦是一樣大的。

機率術語

VAR（variance）方差，Var(x)表示總體/樣本方差，有時也用D(x)表示。只是，平時我們習慣用D來表示方差，例如，Var(X)=9 就表示D(X)=9。

但，二者還是有區別的，因為Var(X)表示X的協方差，如果X是多維的話，結果就是一個協方差矩陣，而不是一個數了，當然若X是一維的，Var(x)與D(x)二者就沒有什麼區別了。

向量自回歸

向量自回歸模型（Vector Autoregression, VAR）

什麼是向量自回歸模型

向量自回歸模型簡稱VAR模型，是一種常用的計量經濟模型，1980年由克里斯托弗·西姆斯（Christopher Sims）提出。VAR模型是用模型中所有當期變數對所有變數的若干滯後變數進行回歸。VAR模型用來估計聯合內生變數的動態關係，而不帶有任何事先約束條件。它是AR模型的推廣，此模型目前已得到廣泛套用。

向量自回歸(VAR)是基於數據的統計性質建立模型，VAR模型把系統中每一個內生變數作為系統中所有內生變數的滯後值的函式來構造模型，從而將單變數自回歸模型推廣到由多元時間序列變數組成的“向量”自回歸模型。VAR模型是處理多個相關經濟指標的分析與預測最容易操作的模型之一，並且在一定的條件下，多元MA和ARMA模型也可轉化成VAR模型，因此近年來VAR模型受到越來越多的經濟工作者的重視。

VAR模型的公式

VAR模型描述在同一樣本期間內的n個變數（內生變數）可以作為它們過去值的線性函式。

一個VAR(p)模型可以寫成為：