若平面到自身的一一變換，使任意對應點的連結線段都通過某定點且被該點平分，則這個一一變換稱為點反射變換，簡稱點反射，定點稱為反射中心或對稱中心，對應點稱為關於反射中心（對稱中心）點對稱點，點反射下的兩個對應圖形稱為關於反射中心（對稱中心）的對稱圖形，簡稱中心對稱圖形。
基本介紹
- 中文名：點反射變換
- 外文名：reflection transformation of in apoint
- 適用範圍：數理科學
簡介,性質,
簡介
點反射變換亦稱點對稱變換或中心對稱變換。一種契約變換。
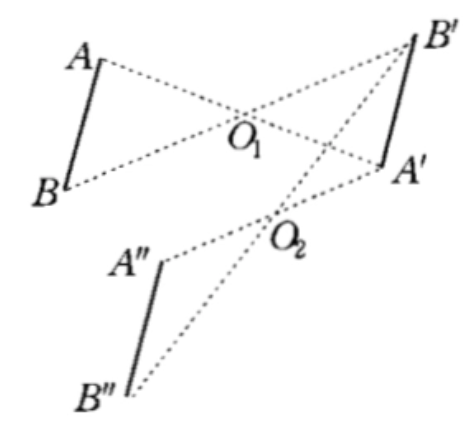
若平面到自身的一一變換，使任意對應點的連結線段都通過某定點且被該點平分，則這個一一變換稱為點反射變換，簡稱點反射，定點稱為反射中心或對稱中心，對應點稱為關於反射中心（對稱中心）點對稱點，點反射下的兩個對應圖形稱為關於反射中心（對稱中心）的對稱圖形，簡稱中心對稱圖形。
性質
點反射有如下主要性質：
1、一一變換 f 是點反射的充分必要條件是，在 f 下對應線段平行、反向且相等；
2、具有不同中心的兩個點反射的乘積是平移變換。如圖1，點 A，B關於 O1 的對稱點分別是 A'，B'，而點 A‘，B’ 關於 O2 對稱點分別是 A''，B''，顯然線段 AB 與 A''B'' 平行、同向且相等，因而，這兩個點反射的乘積是平移變換；
3、點反射的逆變換仍是點反射；
4、反射中心是惟一的一個二重點，通過反射中心點任意一條直線都是二重直線；
5、平移變換與點反射的乘積是關於另一個點為中心的點反射；
6、將中心對稱圖形中任意一個圖形繞對稱中心旋轉 180 度必與其對應圖形重合，因而，旋轉角等於 ±180 度的旋轉是關於旋轉中心的一個點反射。
