基本介紹
- 中文名:空間旋轉變換
- 外文名:rotation transformation in space
- 所屬學科:數學
- 別名:特徵正交變換
- 所屬問題:立體幾何(空間變換)
- 簡介:第一種正交變換
基本介紹








相關介紹















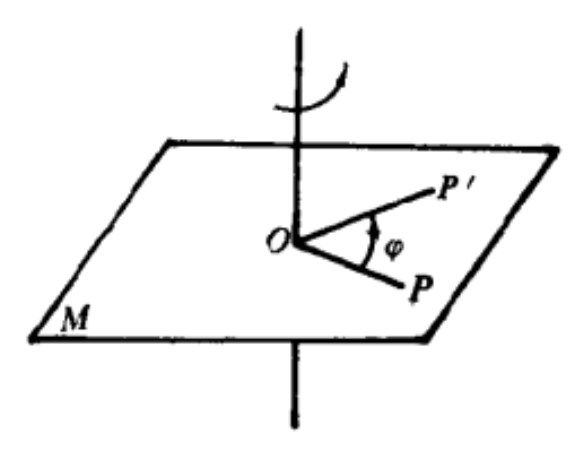



























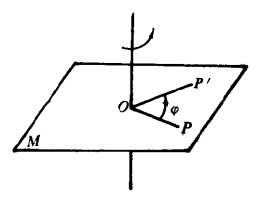
空間旋轉變換(rotation transformation in space)是一種特殊的幾何變換,指空間的所有點繞同一直線旋轉同一角度的變換,亦稱特徵正交變換,是一種特殊的正交變換,n維歐氏空間正交變換的行列式只能是...
旋轉變換是由一個圖形改變為另一個圖形,在改變過程中,原圖上所有的點都繞一個固定的點換同一方向,轉動同一個角度。簡介 簡稱旋轉。歐氏幾何中的一種重要變換.即在歐氏平面上(歐氏空間中),讓每一點P繞一固定點(固定軸線)旋轉一...
羅德里格旋轉公式是計算三維空間中,一個向量繞旋轉軸旋轉給定角度以後得到的新向量的計算公式。這個公式使用原向量,旋轉軸及它們叉積作為標架表示出旋轉以後的向量。可以改寫為矩陣形式,被廣泛套用於空間解析幾何和計算機圖形學領域,成為...
這個映射叫做繞軸S旋轉定角θ的空間旋轉變換。由 到P'P0的旋轉方向規定為:如果θ>0就表示用右手握拳,拇指指向軸上正方向;如果θ 空間旋轉還有空間中心反射。每個點,對於中心O都有它的像與之對應。空間中心反射變換把一個圖形變為...
旋轉法是正投影變換的一種方法,它保持投影面不動,將空間幾何元素繞某一軸線旋轉,使它對投影面處在有利於解題的位置。旋轉法可分為垂直軸旋轉、平行軸旋轉和一般位置軸旋轉。其中旋轉法的套用包括點的旋轉、直線的旋轉和平面的旋轉。
根據定義,環繞著原點的旋轉是一個保持矢量長度,保持空間取向(遵守右手定則或左手定則)的線性變換。定義 在經典力學與幾何學裡,所有環繞著三維歐幾里得空間的原點的旋轉,組成的群,定義為旋轉群。根據定義,環繞著原點的旋轉是一個...
旋轉、伸縮變換w=kz(k≠0),設z=re,k=λe,那么w=rλe。線性變換 線性映射( linear mapping)是從一個向量空間V到另一個向量空間W的映射且保持加法運算和數量乘法運算,而線性變換(linear transformation)是線性空間V到其自身...
空間軸反射變換(axial reflection transformation in space)也稱“空間軸對稱變換”、“空間軸對稱”、“半周旋轉”,是一種特殊的幾何變換,是一種軸反射變換,且是第一種正交變換,指的是空間任一點變為關於同一直線的對稱點的變換。基...
1904年,洛倫茲提出了洛倫茲變換用於解釋邁克耳孫-莫雷實驗。根據他的構想,觀察者相對於以太以一定速度運動時,以太(即空間介質)長度在運動方向上發生收縮,抵消了不同方向上的光速差異,這樣就解釋了邁克耳孫-莫雷實驗的零結果。1905...
(2)線性變換是線性代數研究的一個對象,即向量空間到自身的保運算的映射。例如,對任意線性空間V,位似是V上的線性變換,平移則不是V上的線性變換。對線性變換的討論可藉助矩陣實現。σ關於不同基的矩陣是相似的。Kerσ={a∈V|σ...
幾何變換常常作為圖像處理套用的預處理步驟, 是圖像歸一化的核心工作之一。一個幾何變換需要兩部分運算:首先是空間變換所需的運算, 如平移、縮放、旋轉和正平行投影等, 需要用它來表示輸出圖像與輸入圖像之間的(像素)映射關係;此外,...
這種旋轉並不是三維空間中的那種旋轉,而是嵌入到時間維中一種“四維旋轉”。表現在三維空間中就是有相對運動速度。四維時空間隔是一個標量,標量在坐標變換中肯定是不變的。從數學角度來說,四維時空間隔不變,體現的是閔氏時空的一種...
平面軸反射是第二種正交變換,空間軸反射變換亦稱半周旋轉,它是旋轉角為π的空間繞反射軸的旋轉,因而是第一種正交變換。在軸反射變換下,連結每一對對應點A,A′所得到的線段都垂直於S,且被S所平分,反射軸上的每一點都是不動...
幾何變換可以其操作集合的維度來分類(因此可分類出平面變換與空間變換等)。幾何變換亦可依據其保留其性質來分類:位移保留距離與方向角度;等距同構保留距離與角度;相似保留距離間的比例;仿射變換保留平行;投影變換保留共線性;微分同胚為...
在二維空間中,旋轉可以用一個單一的角 定義。作為約定,正角表示逆時針旋轉。把笛卡爾坐標的列向量關於原點逆時針旋轉 的矩陣是:三維空間 在三維空間中,旋轉矩陣有一個等於單位1的實特徵值。旋轉矩陣指定關於對應的特徵向量的旋轉(歐拉...
正交旋轉,是指因素旋轉的一種。保持因素正交(即不相關)的因素旋轉。相當於對原始因素負荷矩陣作正交變換。這種旋轉保持公共因素方差不變,特殊因素方差也不變。可理解為在因素空間中,因素軸在旋轉過程中保持互相垂直。如何旋轉取決於用...
第八章 三維空間中的剛體運動 8.1 三維歐氏空間上的剛體運動 8.2 剛體變換的表示 8.3 坐標和速度的變換 第九章 三維空間中剛體變換的其他表示方法 9.1 Euler定理和螺旋運動 9.2 旋轉變換的指數坐標表示 9.3 旋轉的四元素和...
這就是空間直角坐標系的移軸公式。從(1)解出 ,就得到移軸的逆變換公式 轉軸變換 設兩個右手坐標系 的原點相同,但坐標向量 和 不同,這時新坐標系可以看成由舊坐標系繞原點旋轉,使得 分別與 重合得到的(如圖2所示),...
在二維空間中,旋轉可以用一個單一的角 定義。作為約定,正角表示逆時針旋轉。把笛卡爾坐標的列向量關於原點逆時針旋轉 的矩陣是:三維空間 在三維空間中,旋轉矩陣有一個等於單位1的實特徵值。旋轉矩陣指定關於對應的特徵向量的旋轉(歐拉...
STNs 能夠自適應地對數據進行空間變換和對齊,使得 CNN 模型對平移、縮放、旋轉或者其它變換等保持不變性。此外,STNs 的計算速度很快,幾乎不會影響原有 CNN 模型的訓練速度,和STNs 模組本身可微,可以無縫嵌入現有網路架構,且無需...
螺旋運動(helicoidal motion)是一種空間變換,指空間中一個旋轉和一個移動方向與旋轉軸平行的平移變換之積。旋轉的軸也稱為螺旋運動的軸,旋轉的角也稱螺旋運動的角。螺旋運動是一種空間運動,其逆變換仍是螺旋運動。兩螺旋運動的積是一...
線性變換的主特徵向量是最大特徵值對應的特徵向量。特徵值的幾何重次是相應特徵空間的維數。有限維向量空間上的一個線性變換的譜是其所有特徵值的集合。例如,三維空間中的旋轉變換的特徵向量是沿著旋轉軸的一個向量,相應的特徵值是1,...
轉軸公式是坐標軸的旋轉公式的簡稱。轉軸公式分為平面直角坐標系中的轉軸公式和空間直角坐標系中的轉軸公式。例如在平面直角坐標系中,不改變原點的位置和坐標軸的長度單位,將兩坐標軸按同一方向繞原點旋轉同一角度的坐標變換叫做坐標軸的...
