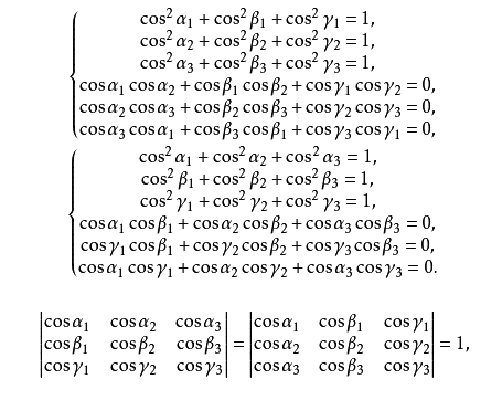空間直角坐標變換

空間直角坐標變換(transformation of rectan-gular coordinates in space)是一類重要的坐標變換，空間中同一點在兩個不同的直角坐標系中的坐標之間的關係，稱為空間直角坐標變換。

基本介紹

• 中文名：空間直角坐標變換
• 外文名：transformation of rectan-gular coordinates in space
• 所屬學科：數學
• 屬性：一類重要的坐標變換
• 相關概念：轉軸變換，移軸變換等

基本介紹

在用坐標法討論變形的時候奔棕，首要的問題是選取一個適當的坐標系來化簡問題，並且常常需要把一個坐標系中的結果轉化到另一個坐標系中去。要解決這個問題，最基本的是求出同一個點在拘慨全汗兩個不同的坐標系中的坐標變換公式。

設在空間給出了兩個右手直角坐標系 ， 和 分別是兩組坐標基向量，它們是空間中的兩組標準正交基。前一個稱為舊坐標系，後一個坐標系稱為新坐標系。它們之間的位置挨榜巴關係完全可以由新坐標系的原點在舊坐標系中的坐標，以及新坐標系的坐標向量在舊坐標系中的坐標所決定。下面先討論直角坐標系的移軸和轉軸(也稱為平移和旋轉)，然後通過移軸和轉軸給出直角坐標變換的一般公式。

移軸變換

設坐標系 的原點 不同， 在舊坐標系中的坐標為 ，但是坐標基向量相同 ，這時新坐標系可以看成由 平移到使 重合而得(如圖1所示)，這種坐標變換稱為移軸變換。

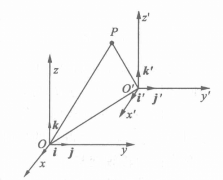圖1 移軸變換

現在推導移軸變換公式，設P為空間任意一點，它在坐標系 中的坐標分別是 ，則有

又 ，代入得

所以

這就是空間直角坐標系的移軸公式。

從(1)解出 ，就得到移軸的逆變換公式

轉軸變換

設兩個右炒舉檔手坐標系 的原點相同，但坐標向量 和 不同，這時新坐標系可以看成由舊坐標系繞原點旋轉，使得 分別與 重合得到的(如圖2所示)，這種坐標變換稱為轉軸變換。

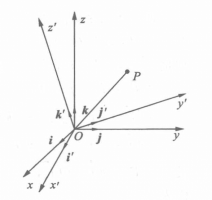圖2 轉軸變換

下面推導轉軸變換公式，具有相同原點的兩坐標系之間的位置關係完全由新、舊坐標軸之間的夾角來決定見表1。軸 軸 ,,, 軸軸墊龍想軸

表1 新、舊坐標系之間的夾角

	軸	軸	軸
軸危戶兆榜	α1	β1	γ1
軸	α2	β2	γ2
軸	α3	β3	γ3

由於都是單位向量，其坐標為它的3個方向餘弦。故從表1可知

設空間任意一點P在舊坐標系中的坐標為，在新坐標系中的坐標為，那么有

由於，由上面兩式得：

將代人得

於是有

這就是空間直角坐標變換的轉軸公式。注意在舊坐標系的請局雄坐標為(3)中的各列係數(行變列)。轉軸的逆變換公式為

正交條件

轉軸變換公式(3)與其逆變換公式(4)都是齊次線性變換，它們的一次項係數不是獨立的，這是因為和是兩組相互垂直的單位向量，它們的坐標要滿足一定的條件，由，且

所以變換公式(3)與逆變換公式(4)的一次項係數分別滿足下列條件：

又因為，可得轉軸變換(3)與(4)的係數行列式

條件(5)，(6)和(7)稱為直角坐標變換的正交條件，根據代數學知識可知，轉軸變換及其逆變換的係數矩陣

是正交矩陣，而且。