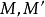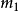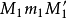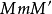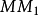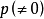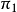基本概念
定義一
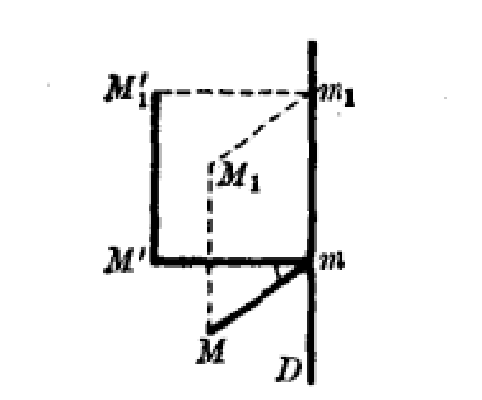
所謂螺旋運動,是指一個旋轉R和一個平移T的合成運動,平移沿著旋轉的軸。這兩個過程的順序無關重要(如果平移不是沿著旋轉的軸,情況就不同了),換言之,設M為一點(如下圖),沿軸D旋轉一個給定的角度至
(這旋轉記作R),再將
平行於D作一確定的平移T到達新位置
;如果先將M用平移T到達
,再將
繞軸D作旋轉R,那么依然來到同樣的位置
。
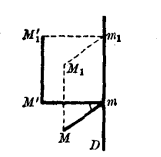 螺旋運動
螺旋運動事實上,設m為兩點
在軸上的公共
射影,而
為
之射影,則圖形
顯然可由圖形
利用平移
得出。那么前者就和後者一樣是一個等腰三角形,它的平面垂直於D而頂角等於R的轉幅,這就證明了斷言的正確性。
螺旋運動顯然包括旋轉(當平移T為零時)和平移(當旋轉R為零時)作為特殊情況。
備註:當我們已知一個螺旋運動時,在軸上就確定了一個正向,即平移的指向。因此,我們說一個螺旋運動是正的(或右手的),或者反過來說是逆的(或左手的),就看沿著平移的正向所作的旋轉是正的還是逆的。
定義二
由繞軸
的旋轉和沿著
方向與旋轉角成比例的移動而合成的運動,稱為
螺旋運動(圖1)。軸
稱為
螺旋軸。
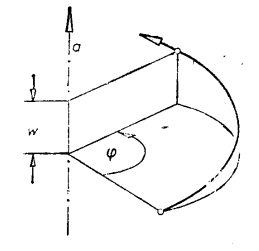 圖1
圖1若
是旋轉角(
螺旋角)而
是進給(
平移距離),則有:
。
比例因子
,稱為
螺旋參數。若順著移動方向觀察一個螺旋,當旋轉為
順時針方向時,這個螺旋為
右螺旋,當旋轉為
逆時針方向時,這個螺旋為
左螺旋。
可以用p的正負號來確定螺旋的方向:
定理1 螺旋運動由繞一條軸的旋轉和沿軸向與旋轉角成比例的移動而形成,它是由螺旋軸,螺旋參數和螺旋方向,(右螺旋或左螺旋)所確定的。
螺旋運動的基本作圖
已知 點
和垂直於
的螺旋軸
的
水平投影和正面投影,螺旋參數p和螺旋角
。
求作 從
轉過螺旋角
至P的這段螺旋軌跡的水平投影和正面投影。
在水平投影中,螺旋運動投影為繞
旋轉
角的轉動:
。
在過
的連繫線上。並比
高出進給
的距離。這段距離
可以往參數圓(圓心為
,半徑為p)上取對應於圓心角
的弧而作出。最好用儘可能短的弦求出這段弧長。 ·
轉過一個整圈
的平移距離
,稱為螺旋的導程。由它可以按照
計算出螺旋參數。p也稱為
轉換導程。
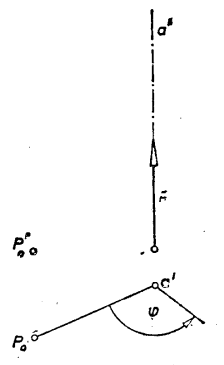 圖2
圖2螺旋體
幾何形體通過螺旋運動形成螺旋體。
點通過螺旋運動形成作為軌跡曲線的螺旋線(軌跡螺旋線);
曲線通過螺旋運動形成為運動曲面的螺旋面;
曲面通過螺旋運動形成為包絡面的螺旋面。
一切螺旋體都可自相旋合。由於這個緣故,它們在工程中得到套用。
螺旋線
1. 以p為螺旋參數,當P點繞軸
作螺旋運動時,其軌跡螺旋線b位於螺旋柱面
(以
為軸、半徑
的迴轉柱面)上。
由於
,所以在
展開後,b成為一條直線。因此,螺旋線b與
的各條素線e相交成定角
,對此有
於是b的切線對
的每個法面
成定坡度。螺旋線b是
同坡線(對
的每個法面而言)。
2. 若將b的切線平移到
上一點R處,則它們形成b的
準錐面(頂點為R、軸線為
和半張角為
的迴轉錐面,圖2)。螺旋運動的兩個導圓
中的“第一個導圓”,稱為螺旋線b的準圓
。準圓平面在R“之下”的距離為p。
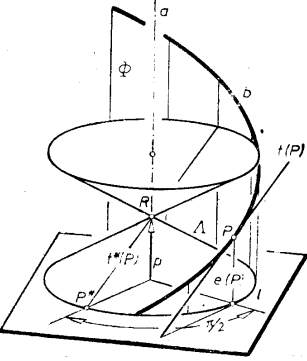 圖3
圖3任一螺旋切線
,都垂直於通過其切點P的螺旋柱面半徑。由此得出:
螺旋切線
平行於通過
準點P*的準錐面素線
,P*在準圓上,與交點
相差
角(圖3)
定理2 每條螺旋線都是螺旋軸的各個法面的同坡線,也是常曲率空間曲線。它的密切平面和切線,都與螺旋軸構成相同的
角。
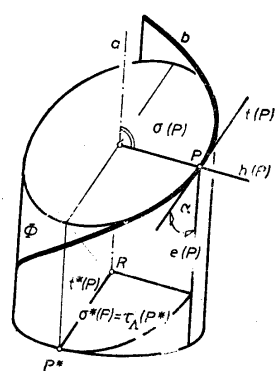 圖4
圖4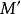
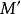
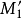
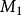
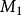
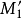
 螺旋運動
螺旋運動


 圖1
圖1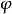
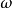
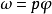
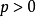
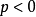
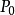
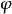
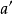
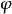
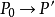
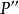
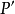
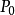
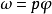
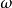
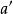
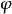
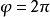
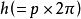
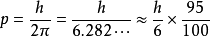
 圖2
圖2
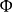

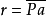
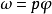
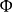
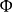
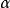
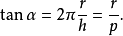



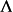

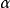
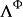
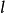
 圖3
圖3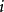
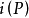
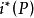
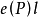
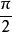
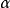
 圖4
圖4