中心反射變換

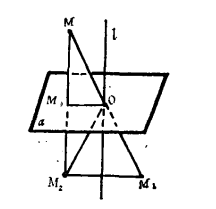
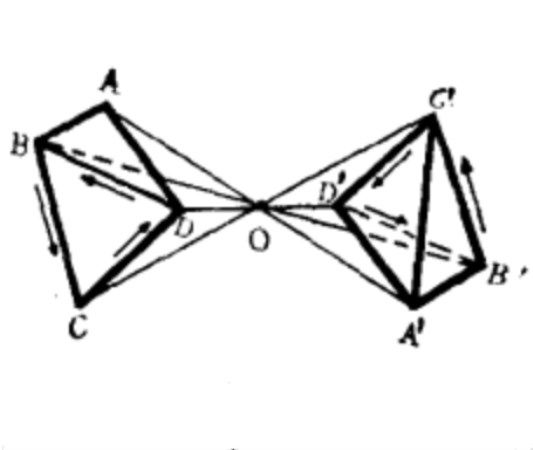
中心反射變換(central reflection transformation)亦稱點反射，簡稱中心反射，是歐氏幾何中的一種重要變換。在歐氏平面或歐氏空間中，把任一點映成與一個給定的點S對稱的點A′的變換稱為關於點S的中心反射變換，點S稱為反射中心或對稱中心。在中心反射下，連結每一對對應點A，A′所得的線段被點S所平分，反射中心S是惟一的不動點，平面上的中心反射是第一種正交變換，空間的中心反射是第二種正交變換。在平面(空間)直角坐標系中，如果以坐標原點為反射中心，則中心反射的代數表達式為：x′=-x，y′=-y，(z′=-z)，其中(x，y(，z))，(x′，y′(，z′))分別是變換前後的點的坐標。

基本介紹

• 中文名：中心反射變換
• 外文名：central reflection transformation
• 所屬學科：數學
• 所屬問題：高等幾何(仿射幾何)
• 別名：點反射，中心反射

基本介紹

設線段的中點為O，則稱M、M₁對稱於O，當M描繪圖形F時，它的對稱點M₁將描繪出圖形F₁，稱為F關於點O的對稱圖形。從F到F₁的變換稱為中心反射變換，或簡稱點反射，記為，即

顯然有中心反射保留任意兩點間的距離不變，因而中心反射是位移，即

但中心反射改變了三面角、四面體的轉向，從而改變了圖形F的轉向(圖1)。

圖1

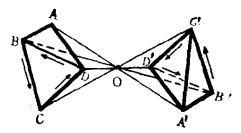
中心反射變換的性質

中心反射有以下性質：

1．中心反射的逆變換是它自己，即

I從而得。這就是說，中心反射變換與它自己的積是恆等變換。

2．兩個中心反射的積是平移。

圖2

證明： 設是兩個反射中心(圖2)，M為任意點，若

則，

則。

由三角形中位線性質定理，可得，

故。

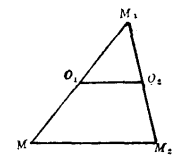
套用舉例

已知直線垂直平面於O點，試證明

證明 因為，

(圖3)，

圖3

所以：，

因而在平面上，為直角三角形，所以。

但，所以。設平面，則

，即是的中垂面，故。