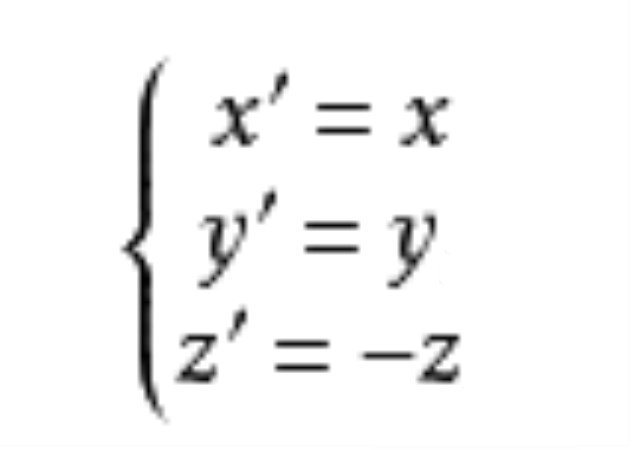鏡面反射變換(mirror reflection transformation)簡稱鏡面反射或平面反射,歐氏空間中的一種特殊變換。在歐氏空間中,把任一點A映成關於給定平面π對稱的點A′的變換稱為關於平面π的鏡面反射變換,平面π稱為反射平面。鏡面反射是第二種正交變換,在鏡面反射變換下,連結變換的每一對對應點A,A′所得到的線段都垂直於反射平面π且被π所平分,平面π上的點都是不動點,鏡面反射變換在直觀上相當於把平面π看做一面鏡子,變換前後的對應點就好比是物與像那樣。
基本介紹
- 中文名:鏡面反射變換
- 外文名:mirror reflection transformation
- 簡稱:鏡面反射或平面反射
- 所屬學科:數學
- 所屬問題:高等代數(歐幾里得空間)
- 別稱:非特徵正交變換,第二類正交變換
基本介紹
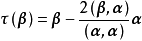

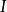


第二類正交變換