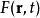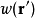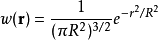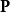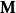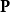麥克斯韋方程組（英語：Maxwell's equations），是英國物理學家詹姆斯·麥克斯韋在19世紀建立的一組描述電場、磁場與電荷密度、電流密度之間關係的偏微分方程。它由四個方程組成：描述電荷如何產生電場的高斯定律、論述磁單極子不存在的高斯磁定律、描述電流和時變電場怎樣產生磁場的麥克斯韋-安培定律、描述時變磁場如何產生電場的法拉第感應定律。
從麥克斯韋方程組，可以推論出光波是電磁波。麥克斯韋方程組和洛倫茲力方程是經典電磁學的基礎方程。從這些基礎方程的相關理論，發展出現代的電力科技與電子科技。
麥克斯韋1865年提出的最初形式的方程組由20個等式和20個變數組成。他在1873年嘗試用四元數來表達，但未成功。現在所使用的數學形式是奧利弗·赫維賽德和約西亞·吉布斯於1884年以矢量分析的形式重新表達的。
基本介紹
- 中文名：馬克士威方程組
- 外文名：Maxwell's equations
- 建立人：詹姆斯·麥克斯韋
- 建立時間：19世紀
概論,高斯定律,高斯磁定律,法拉第感應定律,麥克斯韋-安培定律,方程組匯覽,在真空里的麥克斯韋方程組,微觀尺度與巨觀尺度,數學性質,描述在物質里的電磁性質,束縛電荷和束縛電流,
麥克斯韋方程組（英語：Maxwell's equations）是一組描述電場、磁場與電荷密度、電流密度之間關係的偏微分方程。該方程組由四個方程組成，分別是描述電荷如何產生電場的高斯定律、表明磁單極子不存在的高斯磁定律、解釋時變磁場如何產生電場的法拉第感應定律，以及說明電流和時變電場怎樣產生磁場的麥克斯韋-安培定律。麥克斯韋方程組是因英國物理學家詹姆斯·麥克斯韋而命名。麥克斯韋在19世紀60年代構想出這方程組的早期形式。
在不同的領域會使用到不同形式的麥克斯韋方程組。例如，在高能物理學與引力物理學裡，通常會用到時空表述的麥克斯韋方程組版本。這種表述建立於結合時間與空間在一起的愛因斯坦時空概念，而不是三維空間與第四維時間各自獨立展現的牛頓絕對時空概念。愛因斯坦的時空表述明顯地符合狹義相對論與廣義相對論。在量子力學里，基於電勢與磁勢的麥克斯韋方程組版本比較獲人們青睞。
自從20世紀中期以來，物理學者已明白麥克斯韋方程組不是精確規律，精確的描述需要藉助更能顯示背後物理基礎的量子電動力學理論，而麥克斯韋方程組只是它的一種經典場論近似。儘管如此，對於大多數日常生活中涉及的案例，通過麥克斯韋方程組計算獲得的解答跟精確解答的分歧甚為微小。而對於非經典光、雙光子散射、量子光學與許多其它與光子或虛光子相關的現象，麥克斯韋方程組不能給出接近實際情況的解答。
概論
麥克斯韋方程組是由四個一階線性偏微分方程共同組成。雖然一階與線性都是良好的數學性質，除了具有高度對稱性的案例以外，通常找不到它的解析解，因此必須使用數值方法來找到它的數值解。但由於電動力學是一種線性理論，可以利用疊加原理來求解。
高斯定律
高斯定律描述電場是怎樣由電荷生成。電場線開始於正電荷，終止於負電荷。從估算穿過某給定閉曲面的電場線數量，即電通量，可以得知包含在這閉曲面內的總電荷。更詳細地說，該定律描述穿過任意閉曲面的電通量與這閉曲面內的電荷數量之間的關係。
根據高斯磁定律，磁場線沒有初始點也沒有終止點，而是形成循環或延伸到無窮遠。示意圖展示由流動於圓環導體的電流所形成的磁場線。
高斯磁定律
高斯磁定律表明，磁單極子（磁荷）並不存在於宇宙。在實驗方面，物理學者迄今仍尚未發現磁單極子存在的明確證據。由物質產生的磁場是被一種稱為偶極子的位形所生成。磁偶極子最好是用電流迴路來表示。磁偶極子好似不可分割地被束縛在一起的正磁荷和負磁荷，其淨磁荷為零。磁場線沒有初始點，也沒有終止點。磁場線會形成循環或延伸至無窮遠。換句話說，進入任何區域的磁場線，也必須從那區域離開。以術語來說，通過任意閉曲面的磁通量等於零，磁場是一個螺線矢量場。
法拉第感應定律
麥克斯韋-安培定律
麥克斯韋-安培定律闡明，磁場可以用兩種方法生成：一種是靠電流（最初安培定律描述的方法）產生，另一種是靠隨時間變化的電場（麥克斯韋修正項描述的方法）產生。在電磁學裡，麥克斯韋修正項意味著時變電場可以生成磁場，而由於法拉第感應定律，時變磁場又可以生成電場。這樣，如果時變電場恰好產生了變化的磁場，則根據這兩個方程，這種相互產生的電場和磁場（即電磁波）將可以自我持續在空間裡傳播（更詳盡內容，請參閱條目電磁波方程）。
方程組匯覽
這裡展示出麥克斯韋方程組的兩種等價表述：微觀表述與巨觀表述。
微觀表述專門計算在真空里原子尺度的有限源電荷與有限源電流所產生的電場與磁場。物質可以視為由點電子與點原子核所組成，而內部其它大部分空間都是真空。但是，由於電子與原子核的數量很大，實際而言，無法一一納入計算。事實上，經典電磁學也不需要過度精確的答案。使用微觀麥克斯韋方程組有兩個主要目的，一是推導出巨觀麥克斯韋方程組，二是從原子性質估算出巨觀物質參數，例如電容率、磁導率等等。微觀表述可以給出很多巨觀表述所無法給出的極具價值的信息。
巨觀表述不將物質內部的原子結構納入考量，而是將物質視為一種連續性介質，其性質決定於電容率、磁導率等等巨觀物質參數。從做實驗可以獲得巨觀物質參數與物質的本質、密度、溫度等等的關係。巨觀麥克斯韋方程組可以用來預測帶電粒子、電場與磁場的平均性質。採用這種表述會使得在介電質或磁化物質內各種物理計算更加簡易。
採用不同的單位制，麥克斯韋方程組的形式會稍微有所改變，大致形式仍舊相同，只是不同的常數會出現在方程內部不同位置。國際單位制(SI)是最常使用的單位制，在工程學、化學領域大多都採用這種單位制，大學物理教科書也幾乎都使用這種單位制。其它常用的單位制有高斯單位制、洛倫茲-亥維賽單位制和普朗克單位制。由厘米-克-秒制衍生的高斯單位制，比較適合於教學用途，能夠使得方程看起來更簡單、更易懂。稍後會詳細闡述高斯單位制。洛倫茲-亥維賽單位制也是衍生於厘米-克-秒制，主要用於粒子物理學。普朗克單位制是一種自然單位制，其單位都是根據大自然的性質定義，不是由人為設定。普朗克單位制是研究理論物理學非常有用的工具，能夠在理論論述里給出很大的啟示。
在本條目里，除非特別指出，所有方程都採用國際單位制。
在真空里的麥克斯韋方程組
這種形式的麥克斯韋方程組又稱為“微觀麥克斯韋方程組”，可以用來推導出巨觀麥克斯韋方程組，也可以用來找出原子性質與巨觀性質兩者之間的關聯。
微觀尺度與巨觀尺度
在經典電磁學里，微觀尺度指的是系統尺寸的數量級大於10米的尺度範圍。滿足微觀尺度，電子和原子核可以視為點電荷，微觀麥克斯韋方程組成立；否則，必需將原子核內部的電荷分布納入考量。在微觀尺度計算出來的電場與磁場仍舊變化相當劇烈，空間變化的距離數量級小於10米，時間變化的周期數量級在10至10秒之間。因此，從微觀麥克斯韋方程組，必需經過經典平均運算，才能得到平滑、連續、緩慢變化的巨觀電場與巨觀磁場。巨觀尺度的最低極限為10米。這意味著電磁波的反射與折射行為可以用巨觀麥克斯韋方程組來描述。以這最低極限為邊長，體積為10立方米的立方體大約含有10個原子核和電子。這么多原子核和電子的物理行為，經過經典平均運算，足以平緩任何劇烈的漲落。根據可靠文獻記載，經典平均運算只需要在空間作平均運算，不需要在時間作平均運算，也不需要考慮到原子的量子效應。
經典平均運算是一種比較簡單的平均程式，給定函式
，這函式的空間平均定義為
其中，
是平均運算的空間，
是權重函式。
很多函式都可以選為優良的權重函式，高斯函式正是一例：
最早出現的麥克斯韋方程和其相關理論是為巨觀物質設計的，是一種現象學。在那時候，物理學者並不清楚造成電磁現象的基本原因。後來，按照物質的粒子繪景，才推導出微觀麥克斯韋方程。二十世紀前半期，在量子力學、相對論、與粒子物理學領域的突破與發展，其嶄新理論與微觀麥克斯韋方程組相結合，成為建立量子電動力學的關鍵基石。這是物理學中最準確的理論，所計算出的結果能夠精確地符合實驗數據。
數學性質
麥克斯韋方程組形似超定組：它只涉及到六個未知量（矢量電場、磁場各擁有三個未知量，電流與電荷不是未知量，而是自由設定並符合電荷守恆的物理量），但卻是由八個方程所組成（兩個高斯定律共有兩個方程，法拉第定律與麥克斯韋-安培定律各有三個方程）。經過仔細分析，即可明白，實際上並不是這么簡單。
麥克斯韋方程組的方程具有“獨立性”──從方程組內的任何一個或多個方程，都不能推導出方程組內的任何其它方程。這意味著麥克斯韋方程組不是超定組，其內中沒有重複任何功能的方程。麥克斯韋方程組、洛侖茲力方程與牛頓第二運動定律總合起來具有“完備性”，他們可以說明所有經典電動力學的現象，不需要使用到任何其它方程。在某區域內，給定適當的初始條件與邊界條件，則麥克斯韋方程組的解答具有“唯一性”，即每一個應變數只能有一種函式形式，其內部只含有常數或自變數，不含有任何其它應變數。
法拉第定律與麥克斯韋-安培定律共同主導著在空間內電磁場隨著時間流易的演化，而高斯定律與高斯磁定律則是約束方程，電磁場必須在所有時間與空間遵守這兩個約束方程。理論而言，可以假設某種電磁場在所有空間服從法拉第定律與麥克斯韋-安培定律的指揮，反之，如果他們不遵守高斯定律與高斯磁定律的約束，則它們無法實際存在於真實世界。換句話說，法拉第定律與麥克斯韋-安培定律會給出額外的解答，其不符合高斯定律與高斯磁定律的約束。
描述在物質里的電磁性質
束縛電荷和束縛電流
左半圖展示一群微觀電偶極子，它們所產生的電場，可以視為分別位於最上端與最下端的表面電荷所產生的電場。右半圖展示一群微觀電流迴路共同形成了一個巨觀電流迴路。假若微觀電流迴路均勻分布，則位於內部的電流迴路的貢獻會相互抵銷，但是位於邊界的電流迴路不會被抵銷，因此會形成巨觀的電流迴路。
假設，施加外電場於介電質。施加這個電場的結果是，介電質的分子會形成一個微觀的電偶極子，其伴隨著電偶極矩。分子的原子核會朝著電場的方向稍微遷移位置，而電子則會朝著相反方向稍微遷移位置。這形成了介電質的電極化。如右圖的理想狀況所示，雖然，所有涉及的電荷都仍舊束縛於其原本的分子，由於這些微小遷移所造成的電荷分布，變得好像是在介電質的一邊形成了一薄層正表面電荷，在另一邊又形成了一薄層負表面電荷。電極化強度定義為介電質內部的的電偶極矩密度，也就是單位體積的電偶極矩。在介電質內部，假設電極化強度
是均勻的，則巨觀的面束縛電荷只會出現於介電質表面，即
進入或離開介電質之處；否則，假設
是不均勻的，則介電質內部也會出現束縛電荷。
這些非常複雜與粗糙的束縛電荷與束縛電流的物理行為，在巨觀尺度，可以分別以電極化強度
與磁化強度
來表達。電極化強度與磁化強度分別將這些束縛電荷與束縛電流以恰當的尺度做空間平均，這樣，可以除去單獨整體原子形成的凹凸粗糙結構，但又能夠顯示出強度隨著位置而變化的物理性質。由於所有涉及的矢量場都已做過恰當體積的空間平均，巨觀麥克斯韋方程組忽略了微觀尺度的許多細節。不過，對於了解物質的巨觀尺度性質，這些細節可能不具什麼重要性。
