概述 磁流體力學基本方程組套用於電漿的充分條件是碰撞起支配作用,即粒子碰撞的平均自由程遠小於巨觀變化的特徵長度,而粒子碰撞的時間間隔遠小於巨觀變化的特徵時間。磁流體力學基本方程組包括考慮介質運動的電動力學方程組和考慮磁場力的流體力學基本方程組。但在許多情況下,必須把電動力學方程組中的歐姆定律推廣為廣義歐姆定律,即把導電氣體當作電子、帶電粒子和中性粒子三種不同的單獨流體,考慮氣體中的電流與電磁場的關係;在流體力學基本方程組中的運動方程上必須添加電磁場作用於導電流體的力,即洛倫茲力;在能量方程上必須添加電磁場引起的熱能增加率。
電動力學方程組 電動力學方程組 包括麥克斯韋方程組、洛倫茲力公式和廣義歐姆定律。
麥克斯韋方程組 英國物理學家J.C.麥克斯韋首先總結出來的電磁場運動普遍規律的數學表達式。對於介質內部,麥克斯韋方程組為:
式中
D =ε
E ,
B =μ
e H ;
E 、
D 、
B 、
H 、
J 、ρ
e 、ε和μ
e 分別為電場強度、電位移、磁感應強度、磁場強度、傳導電流密度、自由電荷密度、電容率和磁導率。方程組採用有理化米·千克·秒·安培制。在真空或不導電介質中
J =0的情況下,如果已知電磁場的初始狀態以及必要的邊界條件,則以後任何時刻電磁場的狀態僅用麥克斯韋方程組即可確定。取式(1)的散度,得 可見式(2)是積分此方程的初始條件,不是一個獨立的方程;取式(3)的散度並利用式(4),得電荷守恆方程:
,故式(3)和式(4)已包含電荷守恆定律。
在良導電流體中的任何點不可能有電荷堆積,因此不能通過式(4)來計算電場,但是可以利用歐姆定律:
式中
v 為流體速度;m和e為電子的質量和電荷;n為單位體積流體中的電子數;σ為電導率。 上式是經過修正的,它考慮了運動流體切割磁力線所產生的感應電場和電子慣性的影響。在電子的低頻振盪情況下,上式右端最後一項可以省略;在良導電流體中,可以不必考慮位移電流
。在上述條件下,取式(5)兩端的旋度並利用麥克斯韋方程組消去E,就得到:
上式右端第一項代表磁傳輸效應,即磁力線和流體一同運動(見磁凍結定理);右端第二項代表磁擴散效應,即流體和磁力線相對滑移。磁雷諾數就是一種量度電漿中磁擴散效應和磁傳輸效應相對重要性的無量綱參數,定義為
R m =
Luσμ e ,式中
L 和
U 分別為可與磁場尺度相比的特徵長度和可與粒子實際速度相比的特徵速度。若
,則磁力線凍結於電漿之中,這是宇宙中電漿的普遍情況;若
,則磁力線很容易滑過電離物質,這是實驗室電漿的普遍情況。因此,在實驗室中很難進行模擬天體問題的實驗。
洛倫茲力公式 H.A.洛倫茲根據實驗結果提出,不論帶電體的運動狀態如何,力密度f都由下式決定:
式(7)即稱為洛倫茲力公式,式中右端第一項代表單位體積流體中的電荷所受的電場力;第二項代表上述電荷運動形成的電流所受的磁場力。E B v ⊥ σB 和σE×B v 寑的方向相反;後者為電場導致的磁場力,它垂直於電場和磁場。
廣義歐姆定律 式(5)給出的是簡化的歐姆定律,它沒有考慮磁場力以及在溫度梯度和壓力梯度下電子和離子不同擴散率的影響。描述電流密度同上述因素以及電場、磁場、速度間依賴關係的方程稱為廣義歐姆定律。
磁場力的分解 在磁場中,帶電粒子繞磁力線作螺旋運動,螺線中心沿E×B方向漂移。若B很小,離子漂移比電子漂移小很多,可以略去,而電子漂移產生霍耳效應(見磁流體發電)。這時,廣義歐姆定律可寫成:
式中pe 為電子氣的分壓;右端第四項為電子擴散導致的電場,同E J B J ⊥ 為霍耳電流密度。若B
式中下標⊥和∥代表垂直和平行於磁場的量;
σ ⊥ ≈
σ /
2 ,T為溫度;k為熱導率。
對於部分電離電漿(完全電離電漿和中性氣體的混合物)的廣義歐姆定律,則必須在式(8)的右端附加一個考慮中性粒子影響的修正項。
修正的流體力學基本方程組 由於磁場對良導電流體的影響,流體力學基本方程組應作如下修正:
連續性方程
運動方程
氣體狀態方程
P =RσT , (11)
能量方程
式中Ф為粘性耗散功率,其定義為:
p 、
ρ 、
T 、
μ 、
k 、
c p 和
R 分別為壓強、密度、溫度、動力粘性係數、熱導率、定壓比熱和氣體常數;
。式(9)說明質量守恆,即質量流的散度等於密度減少率。式(10)說明單位體積流體所受的力等於負的壓強梯度、粘性力密度和磁場力(密度)之和。式(12)說明能量守恆,即單位體積中流體焓的隨體變化率等於壓強的隨體變化率、熱傳導功率、粘性耗散功率以及焦耳熱產生率之和。式(9)、(10)、(11)、(12)是包含
p 、
ρ 、
T 、
v 等6個變數的6個方程,磁場可由式(6)給出,所以磁流體力學方程組是封閉的。
初始和邊界條件
套用以上方程來解決實際問題,必須給出實際問題的初始條件和邊界條件。一般磁流體力學問題不是先給出初始時刻各物理變數的空間分布函式,而是要求初始條件必須同初始邊界條件和基本方程組一致。磁流體力學的邊界條件除流體力學中的邊界條件(如在物體表面流速為零)之外,還有電磁場邊界條件。在流體邊界(例如固體邊界)上,介質的物理性質發生間斷性變化,在間斷面上要求電磁邊界條件滿足:①磁感應強度的法向分量連續;②電場強度的切向分量連續;③在有限電導率情況下,磁場強度連續;若σ →∞,則允許出現面電流和磁場強度間斷;④邊界上電位移的法向分量可發生間斷,即邊界上具有自由面電荷。
參考書目 T.J.M.博伊德、J.J.桑德森著, 戴世強、 陸志雲譯:《電漿動力學》,科學出版社,北京,1977。(T.J.M.Boyd and J.J.Sanderson,, Nelson,London,1969.)


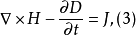








 磁場力的分解
磁場力的分解