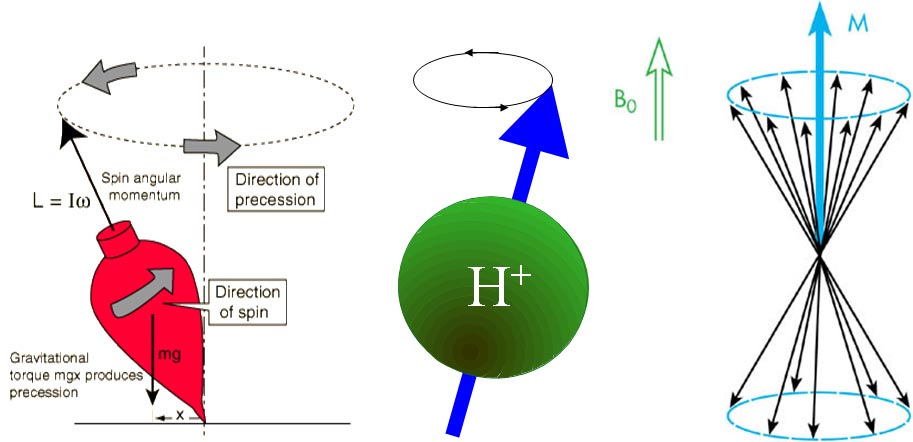
概述
磁矩是磁鐵的一種物理性質。處於外磁場的
磁鐵,會感受到
力矩,促使其磁矩沿外磁場的磁場線方向排列。磁矩可以用
矢量表示。磁鐵的磁矩方向是從磁鐵的指南極指向指北極,磁矩的大小取決於磁鐵的磁性與量值。不只是磁鐵具有磁矩,
載流迴路、
電子、
分子或
行星等等,都具有磁矩。
科學家至今尚未發現宇宙中存在有
磁單極子。一般
磁性物質的磁場,其泰勒展開的多極展開式,由於
磁單極子項目恆等於零,第一個項目是
磁偶極子項、第二個項目是磁四極子(quadrupole)項,以此類推。磁矩也分為磁偶極矩、磁四極矩等等部分。從磁矩的磁偶極矩、磁四極矩等等,可以分別計算出磁場的磁偶極子項目、磁四極子項目等等。隨著距離的增遠,磁偶極矩部分會變得越加重要,成為主要項目,因此,磁矩這術語時常用來指稱磁偶極矩。有些教科書內,磁矩的定義與磁偶極矩的定義相同。
計算公式
其中,
為磁偶極矩,
為電流,
為面積矢量。磁偶極矩、面積矢量的方向是由
右手定則決定。
處於外磁場的載流循環,其感受到的力矩和其
勢能與磁偶極矩的關係為:
許多
基本粒子,例如
電子,都具有
內稟磁矩。這種內稟磁矩是許多巨觀磁場力的來源,許多物理現象也和此有關。這種磁矩和經典物理的磁矩不同,而是和粒子的
自旋有關,必須用
量子力學來解釋。這些內稟磁矩是
量子化的,最小的基本單位,常常稱為“
磁子”(magneton)。例如,電子
自旋的磁矩與
玻爾磁子的關係式為:
兩種磁源
在任何物理系統里,磁矩最基本的源頭有兩種:
電荷的運動,像電流,會產生磁矩。只要知道物理系統內全部的電流密度分布(或者所有的電荷的位置和速度),理論上就可以計算出磁矩。
像電子、
質子一類的基本粒子會因自旋而產生磁矩。每一種基本粒子的內稟磁矩的大小都是常數,可以用理論推導出來,得到的結果也已經通過做實驗核對至高準確度。例如,電子磁矩的測量值是−9.284764×10焦耳/特斯拉。磁矩的方向完全決定於粒子的自旋方向(電子磁矩的測量值是負值,這意味著電子的磁矩與自旋呈相反方向)。
整個物理系統的淨磁矩是所有磁矩的矢量和。例如,
氫原子的磁場是以下幾種磁矩的矢量和:
電子的自旋。
電子環繞著質子的軌域運動。
質子的自旋。
再舉個例子,構成條形磁鐵的物質,其未配對電子的內稟磁矩和軌域磁矩的矢量和,是條形磁鐵的磁矩。
定義
在原子中,電子因繞
原子核運動而具有軌道磁矩;電子因自旋具有
自旋磁矩;原子核、質子、
中子以及其他基本粒子也都具有各自的自旋磁矩。這些對研究
原子能級的
精細結構,磁場中的
塞曼效應以及磁共振等有重要意義,也表明各種基本粒子具有複雜的結構。
分子的磁矩就是電子軌道磁矩以及電子和核的自旋磁矩構成的(
μ=
μs+
μl=
gsps+glpl),
磁介質的磁化就是外磁場對分子磁矩作用的結果。
粒子的內稟屬性。每種粒子都有確定的內稟磁矩。自旋為s的
點粒子的磁矩μ由μ=g(e/2m)p給出,式中e和m分別是該粒子的電荷和質量,g是一個數值因子,p為自旋角動量。自旋為零的
粒子磁矩為零。自旋為1/2的粒子,g=2;自旋為1的粒子,g=1;自旋為3/2的粒子,g=2/3。理論上普遍給出g=1/s。
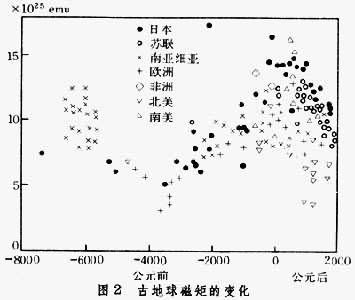 古地球磁矩的變化
古地球磁矩的變化 粒子磁矩可通過實驗測定。但實驗測定結果並不與此相符,其間差別稱為反常磁矩。對於自旋均為1/2的電子、
μ子、
質子和中子,精確測定其g因子分別為
電子 gl2=1.001159652193(10)
μ子 gl2=1.001165923(8)
質子 gl2=2.792847386(63)
中子 gl2=-1.91304275(45)
粒子反常磁矩的來源有二:一是
量子電動力學的輻射修正,電子、μ子屬於這種情形,即使是點粒子,粒子產生的電磁場對其自身的作用導致自旋磁矩的微小變化,這一改變可以嚴格地用量子電動力學精確計算,結果與實驗測定符合得很好;另一是由於粒子有內部結構和強相互作用的影響,質子和中子屬於這種情形,質子和中子的反常磁矩用於分析其內部結構。
各類磁矩
載流迴路磁矩
在一個載流迴路中,磁矩大小是電流乘以迴路面積:u=I×S;
其中,u為磁矩,I 為電流,S 為面積。
M=u×B 其中,B 為磁感應強度。
基本粒子磁矩
許多
基本粒子(例如電子)都有內稟磁矩,這種磁矩和經典物理的磁矩不同,必須使用
量子力學來解釋它,和粒子的
自旋有關。而這種內稟磁矩即是許多在巨觀之下磁力的來源,許多的
物理現象也和此有關。這些內稟磁矩是
量子化的,也就是它有最小的基本單位,常常稱為“
磁子”(magneton)或
磁元,例如電子自旋磁矩的矢量絕對值即和
玻爾磁子成比例關係:
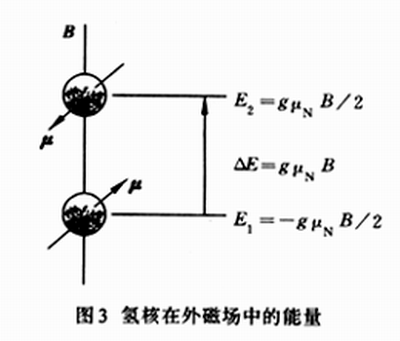 核自旋與核磁矩
核自旋與核磁矩其中為電子自旋磁矩,電子自旋g因子
gs是一項比例常數,
為玻爾磁子,
s為電子的自旋角動量。
基本粒子
在
原子物理學和
核子物理學裡,磁矩的大小標記為
,通常測量單位為
玻爾磁子或
核磁子(nuclear magneton)。磁矩關係到粒子的自旋,和/或粒子在系統內的軌域運動。以下列表展示出一些粒子的內稟磁矩:
| 粒子 | 內稟磁矩(10焦耳/特斯拉) | 自旋量子數 |
|---|
| -9284.764 | 1/2 |
| +14.106067 | 1/2 |
| -9.66236 | 1/2 |
| -44.904478 | 1/2 |
| +4.3307346 | 1 |
| +15.046094 | 1/2 |
欲知道更多有關於磁矩與磁化強度之間的物理關係,請參閱條目
磁化強度。
載流迴路產生的磁場
磁偶極子的磁場線。從側面望去,磁偶極子豎立於繪圖的中央。
載流迴路會在周圍產生磁場。這磁場包括偶極磁場與更高次的多極項目。但是,隨著距離的增遠,這些多極項目會更快速地減小,因此,在遠距離位置,只有偶極項目是磁場的顯要項目。
思考一個載有恆定電流
的任意局域迴路
,其
磁矢勢為
其中,
是檢驗位置,
是源頭位置,是微小線元素
的位置,
是
磁常數。
所以,磁矢勢展開為
由於閉合迴路的矢量線積分等於零,磁單極子項目恆等於零。
由於磁偶極子的矢勢有一個
奇點在它所處的位置(原點
),必須特別小心地計算,才能得到正確答案。更仔細地推導,可以得到磁場為
偶極磁場的狄拉克δ函式項目造成了原子
能級分裂,因而形成了
超精細結構(hyperfine structure)。在
天文學里,
氫原子的超精細結構給出了21公分譜線,在
電磁輻射的
無線電波範圍,是除了
3K背景輻射以外,宇宙瀰漫最廣闊的電磁輻射。從複合紀元(recombination)至再電離紀元(reionization)之間的天文學研究,只能依靠觀測21公分譜線無線電波。
給予幾個磁偶極矩,則按照
疊加原理,其總磁場是每一個磁偶極矩的磁場的總矢量和。
磁偶極子感受到的磁力矩
處於均勻磁場的一個方形載流循環。
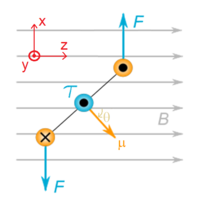
如圖右,假設載有電流
的一個方形循環處於外磁場
。方形循環四個邊的邊長為
,其中兩個與
平行的邊垂直於外磁場,另外兩個邊與磁場之間的夾角角弧為
。
垂直於外磁場的兩個邊所感受的磁力矩為
另外兩個邊所感受的磁力矩互相抵消。注意到這循環的磁偶極矩為
。所以,這循環感受到的磁力矩為
令載流循環的面積趨向於零、電流趨向於無窮大,同時保持
不變,則這載流循環趨向於理想磁偶極子。所以,處於外磁場的磁偶極子所感受到的磁力矩也可以用上述方程表示。
當磁偶極矩垂直於磁場時,磁力矩的大小是最大值
;當磁偶極矩與磁場平行時,磁力矩等於零。
螺線管的磁矩
一個多匝線圈(或
螺線管)的磁矩是其每個單匝線圈的磁矩的矢量和。對於全同匝(單層卷繞),只需將單匝線圈的磁矩乘以匝數,就可得到總磁矩。然後,這總磁矩可以用來計算磁場,力矩,和儲存能量,方法與使用單匝線圈計算的方法相同。
假設螺線管的匝數為
,每一匝線圈面積為
,通過電流為
,則其磁矩為
電子的磁矩
電子和許多其它種類的粒子都具有內稟磁矩。這是一種
量子屬性,涉及到
量子力學。詳盡細節,請參閱條目
電子磁偶極矩(electron magnetic dipole moment)。微觀的內稟磁矩集聚起來,形成了巨觀的磁效應和其它物理現象,例如
電子自旋共振。
電子的磁矩是
其中,
是電子的朗德g因子,
是
玻爾磁子,
是電子的自旋角動量。
按照
前面計算的經典結果,
;但是,在狄拉克力學裡,
;更準確地,由於
量子電動力學效應,它的實際値稍微大些,
。
請注意,由於這方程內的負號,電子磁矩與自旋呈相反方向。對於這物理行為,
經典電磁學的解釋為:假想自旋角動量是由電子繞著某旋轉軸而產生的。因為電子帶有負電荷,這旋轉所產生的電流的方向是相反的方向,這種載流迴路產生的磁矩與自旋呈相反方向。同樣的推理,帶有正電荷的正子(電子的
反粒子),其磁矩與自旋呈相同方向。
原子的磁矩
在原子內部,可能會有很多個電子。多電子原子的總角動量計算,必須先將每一個電子的自旋總和,得到總自旋,再將每一個電子的軌角動量總和,得到總軌角動量,最後用
角動量耦合(angular momentum coupling)方法將總自旋和總軌角動量總和,即可得到原子的總角動量。原子的磁矩
與總角動量
其中,
是總角動量對於磁場方向的分量,
是
磁量子數,可以取2J+1個整數値,-J、 -J+1、…、J-1、J,之中的任意一個整數值。
處於磁場的磁偶極子的
動力學,不同於處於
電場的
電偶極子的動力學。磁場會施加力矩於磁偶極子,迫使它依著磁場線排列。但是,力矩是角動量對於時間的導數。所以,會產生自旋
進動,也就是說,自旋方向會改變。這物理行為以方程表達為
其中,
是迴轉磁比率(gyromagnetic ratio) ,
是磁場。
注意到這方程的左手邊項目是角動量對於時間的導數,而右手邊項目是力矩。磁場又可分為兩部分:
其中,
是有效磁場(外磁場加上任何自身
是
阻尼係數。
這樣,可以得到蘭道-李佛西茲-吉爾伯特方程(Landau–Lifshitz–Gilbert equation):
方程右邊第一個項目描述磁偶極子繞著有效磁場的進動,第二個項目是阻尼項目,會使得進動漸漸減弱,最後消失。蘭道-李佛西茲-吉爾伯特方程是研究磁化動力學最基本的方程之一。
原子核的磁矩
核子系統是一種由
核子(
質子和
中子)組成的精密物理系統。自旋是核子的量子性質之一。由於
原子核的磁矩與其核子成員有關,從核磁矩的測量數據,更明確地,從核磁偶極矩的測量數據,可以研究這些量子性質。
雖然有些
同位素原子核的
激發態的衰變期超長,大多數常見的原子核的自然存在狀態是
基態。每一個同位素原子核的能態都有一個獨特的、明顯的核磁偶極矩,其大小是一個常數,通過細心設計的實驗,可以測量至非常高的精確度。這數值對於原子核內每一個核子的獨自貢獻非常敏感。若能夠測量或預測出這數值,就可以揭示核子
波函式的內涵。現今,有很多理論模型能夠預測核磁偶極矩的數值,也有很多種實驗技術能夠進行原子核測試。
分子的磁矩
任何分子都具有明確的磁矩。這磁矩可能會跟分子的能態有關。通常而言,一個分子的磁矩是下列貢獻的總和,按照典型強度從大至小列出:
假若有未配對電子,則是其自旋所產生的磁矩(
順磁性貢獻)
電子的軌域運動,處於基態時,所產生常與外磁場成正比的磁矩(
抗磁性貢獻)
分子磁性範例
氧分子,O
2,由於其最外面的兩個未配對電子的自旋,具有強順磁性。
二氧化碳分子,CO
2,由於電子軌域運動而產生的,與外磁場成正比的,很微弱的磁矩。在某些稀有狀況下,假若這分子是由具磁性的同位素組成,像C或O,則此同位素原子核也會將其核磁性貢獻給分子的磁矩。
氫分子,H
2,處於一個弱磁場(或零磁場),會顯示出核磁性。氫分子的兩種自旋
異構體,
正氫或
仲氫,都具有這種物理性質。






 古地球磁矩的變化
古地球磁矩的變化 核自旋與核磁矩
核自旋與核磁矩