原子磁矩是原子內部各種磁矩總和的有效部分。原子的磁矩是物質磁性的來源,而原子的磁矩又主要來自於電子的自旋磁矩和軌道磁矩的貢獻。
基本介紹
介紹
磁矩定義
電子磁矩
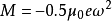
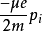

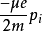


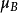





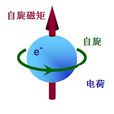
原子磁矩是原子內部各種磁矩總和的有效部分。原子的磁矩是物質磁性的來源,而原子的磁矩又主要來自於電子的自旋磁矩和軌道磁矩的貢獻。
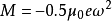
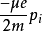

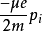


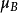





原子磁矩是原子內部各種磁矩總和的有效部分。原子的磁矩是物質磁性的來源,而原子的磁矩又主要來自於電子的自旋磁矩和軌道磁矩的貢獻。...
分子磁矩是指分子中的電子自旋磁矩與電子軌道磁矩的總和。它是物質的微觀性質。近代物理理論和實驗研究表明,電子有磁矩,原子和原子核一般也有磁矩。原子中電子繞核的...
感生磁矩是指一些材料(如鹼金屬)本身不具有自發磁性,外層電子之間不存在交換作用,但是在磁場中會產生一定的磁矩就叫做感生磁性。該材料也因而具有較弱的順磁性。...
原子能級是指原子系統能量量子化的形象化表示。按照量子力學理論,可計算出原子系統的能量是量子化的,能量取一系列分立值;能量值取決於一定的量子數,因此能級用一定...
玻爾磁子或稱玻爾磁元,以物理學家尼爾斯·玻爾為名,是根據量子力學理論所得,與電子相關的磁矩基本單位,是一項常數。其用在電子軌域角動量及自旋角動量相關磁性的...
軌道磁矩,是指材料內部電子的循軌運動和自旋運動都可以看作是一個閉合的環形電流,因而必然產生磁矩,由電子循軌運動產生的磁矩。電子軌道運動產生的磁矩與動量矩在...
磁結構通常指晶體中原子磁矩空間取向的周期性和對稱性,或具有某種規律性分布。磁結構相對於磁矩無規取向的情況來說,磁矩在空間的規律性分布又稱為磁有序。這一...
一般,在鐵磁共振情況下,外加恆定磁場已使鐵磁體飽和磁化,即參與鐵磁共振進動運動的是彼此平行的原子磁矩(飽和磁化強度Ms)。鐵磁共振的這一特點引起的主要效應是...
內容簡介全書共分17章,各章均附有習題。前7章為原子物理部分,作者從光譜學、電磁學、x射線等方面的實驗事實總結出的規律匯總到原子結構的全貌。第8章~第16章...
