基本介紹
- 中文名:軌道磁矩
- 外文名:orbital magnetic moment
- 領域:物理
- 全稱:電子軌道磁矩
- 性質:磁矩
- 定義:電子繞核的運動產生的磁矩
概念
計算
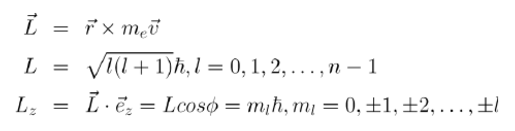

磁性
磁矩


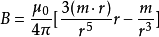
動量矩
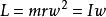
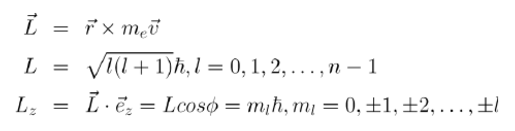



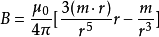
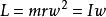
軌道磁矩,是指材料內部電子的循軌運動和自旋運動都可以看作是一個閉合的環形電流,因而必然產生磁矩,由電子循軌運動產生的磁矩。電子軌道運動產生的磁矩與動量矩在...
描述載流線圈或微觀粒子磁性的物理量。平面載流線圈的磁矩定義為m=iSn式中i電流強度;S為線圈面積;n為與電流方向成右手螺旋關係的單位矢量。在均勻外磁場中,平面...
原子磁矩是原子內部各種磁矩總和的有效部分。原子的磁矩是物質磁性的來源,而原子的磁矩又主要來自於電子的自旋磁矩和軌道磁矩的貢獻。1...
電子自旋磁矩是電子的內稟角動量和磁矩。1925年烏侖貝克和古茲密特假設:電子具有自旋角動量ћ/2,並具有與E之相聯繫的一個玻爾磁子的自旋磁矩μB。...
感生磁矩是指一些材料(如鹼金屬)本身不具有自發磁性,外層電子之間不存在交換作用,但是在磁場中會產生一定的磁矩就叫做感生磁性。該材料也因而具有較弱的順磁性。...
當鐵磁層非常薄的時候,原子中的軌道各向異性得體現,就有可能使得界面各向異性超過形狀各向異性,從而實現了垂直磁各向異性。可以利用該性質套用於垂直磁各向異性磁性...
分子磁矩是指分子中的電子自旋磁矩與電子軌道磁矩的總和。它是物質的微觀性質。近代物理理論和實驗研究表明,電子有磁矩,原子和原子核一般也有磁矩。原子中電子繞核的...
顯示抗磁性的物質的原子、離子或分子中的電子在基態都是成對的配合了的,它們的自旋磁矩和軌道磁矩各互相抵消。超導電性材料在外磁場中被冷至其臨界溫度以下時,體...
是由於外磁場對電子的軌道磁矩和自旋磁矩的作用,或使能級分裂才產生的。其中譜線分裂為2條(順磁場方向觀察)或3條(垂直於磁場方向觀察)的叫正常塞曼效應;3條以上...
他認為,由於電子存在軌道磁矩,並且磁矩方向在空間的取向是量子化的,因此在磁場作用下能級發生分裂,譜線分裂成間隔相等的3條譜線。塞曼和洛侖茲因為這一發現共同...
拉莫爾進動Larmor precession是指電子、原子核和原子的磁矩在外部磁場作用下的進動。...
在晶體中,電子的軌道磁矩受晶格的作用,其方向是變化的,不能形成一個聯合磁矩,對外沒有磁性作用。因此,物質的磁性不是由電子的軌道磁矩引起,而是主要由自旋磁矩引起...
