基本介紹
- 中文名：原子能級
- 外文名：atomic energy levels
- 描述：原子系統能量量子化的形象化表示
- 學科：量子力學
- 分類：物理
基本介紹,結構,影響,研究進展,理論模型,結論,
基本介紹
能級取決於原子的電子組態，此外還取決於原子內相互作用的耦合類型，在LS耦合情形下，總軌道角動量、總自旋和總角動量的量子數L、S、J都是好量子數，能級標記為一定的符號。例如：氦原子某能級符號表示為1s2p3p2，其中左邊部分1s2p為電子組態，大寫拉丁字母分別對應於L=0、1、2、3、…的拉丁字母S、P、D、F…左上角的數值為2S+1，表示多重態的重數，右下角的數值是J值。在磁場中原子磁矩與磁場的相互作用導致能級分裂，還須用相應的磁量子數分別予以標記。
結構
非典型耦合下二價原子能級的精細結構
典型耦合(LS及jj耦合)下，二價原子能級的精細結構問題已被解決。然而，一般來說，LS耦合只適用於電子與核之間的磁相互作用遠小於電子間靜電相互作用( 非有心力部分)的情形；jj 耦合只適用於電子與核之間的磁相互作用遠大於電子間靜電相互作用( 非有心力部分)的情形。 遺憾的是，許多二價原子的精細結構能級既不歸屬於LS 耦合也不歸屬於 jj 耦合。這個問題早已在實驗中發現且已總結出許多實驗數據。理論上也有一些研究，但多局限於某些具體原子或某幾類具體電子組態，沒有給出完整的理論體系。相關研究試圖在典型耦合理論基礎上，給出在非典型耦合下計算二價原子精細結構能級的一般理論，而典型耦合下的結果將作為非典型耦合的特例。
組態能級精細結構圖
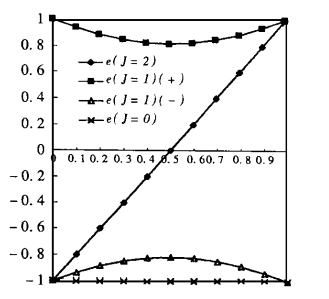組態能級精細結構圖在典型耦合理論基礎上，給出了在非典型耦合下計算二價原子精細結構能級的理論公式，並將理論套用到若干具體問題，結果與實驗數據相符，且直觀地顯示出典型耦合只是非典型耦合的特例。
影響
電漿禁止效應對原子能級的影響
研究進展
在實驗技術的推動下，高電離的高荷離子的實驗觀測與理論研究重新引起了人們的興趣，人們在這方面已經開展了不少工作。其中，非常重要的一項工作就是準確地確定元素在電漿環境中的能級結構和振子強度。這些原子數據在電漿診斷以及電漿輻射不透明度研究中發揮著重要作用，比如，Brage等人曾指出具有相同初態且末態能量相近的兩個躍遷的振子強度的比值可用於電漿中局域電子密度的診斷；Rubiano等人曾使用氫的禁止模型計算鋁的輻射躍遷等原子數據，進而用於鋁的輻射不透明度的計算；saha等人也曾提到類Be元素的譜線強度可以用於電漿的溫度和密度的診斷。
實際電漿中含有大量的自由電子和各個價態的離子，要想準確地計算電漿禁止效應對能級結構和振子強度的影響是很困難的。通常採用的方法是對電漿環境的作用進行平均從而得出一個較為簡單的表達式，進而使得計算過程大大簡化。通常用以下兩種模型來計算電漿環境中各個價態離子的特性：第一種是利用考慮了溫度效應和密度效應的自洽場模型來求出勢函式。但是這種考慮了電漿禁止效應的自洽場需要循環疊代才能求出，如果需要計算大量的原子數據，那么計算時間就會很長。第二種方法是找出考慮了電漿禁止效應的勢函式的解析表達式，Debye模型就是其中的一種。它的基本思想是假設考慮了電漿禁止效應的電場勢是由球對稱的電荷分布決定的，並且假設粒子的動能遠遠大於粒子之間的勢能，粒子在電漿中的分布滿足Boltzmann統計，從而在Debve一級近似下從球對稱的Poisson方程得到Debye禁止勢。自Debye等人於1923年提出Debye模型以來，它在原子分子領域得到了廣泛套用。Debve模型不僅能用於計算類氫離子的各種截面、譜線位移和線型，而且經過改進的模型可以用於多電子體系的研究。特別是最近幾十年來，人們利用Debve模型做了大量的工作來研究電漿禁止效應對類氫，類氦，多電子體系元素的原子結構的影響。其中，Rubiano等人、Bielinska-Waz等人、Rodrfguez等人、Saha等人考慮了相對論效應對原子輻射特性的影響。但是，對於電漿中類Be中Z元素原子結構的研究卻是很少的。
相關研究利用考慮了電漿禁止效應的全相對論的MCDF(multi—cofiguration Dirac-Fork)模型，通過改
進的GRASP2程式計算了MnXXII-BrXXXII等11個類Be離子的能級結構和振子強度，重點討論了最低兩個組態的2s2一[2s1/2，2p1/2]1和2s2一[2s1/2，2p3/2]1的躍遷，給出了它們在不同電漿禁止條件下的能級和振子強度的變化情況。這兩條對電漿診斷極其重要的譜線都曾在天體物理以及實驗室中被人們大量觀測到。
進的GRASP2程式計算了MnXXII-BrXXXII等11個類Be離子的能級結構和振子強度，重點討論了最低兩個組態的2s2一[2s1/2，2p1/2]1和2s2一[2s1/2，2p3/2]1的躍遷，給出了它們在不同電漿禁止條件下的能級和振子強度的變化情況。這兩條對電漿診斷極其重要的譜線都曾在天體物理以及實驗室中被人們大量觀測到。
理論模型
對於複雜的原子，組態相互作用(configure interaction，CI)在原子結構計算中起了非常重要的作用，但在實際計算中，不可能包括所有可能的組態相互作用，通常通過控制電子激發數目來選取組態。在考慮組態相互作用時，只包含了最多只能有兩個電子向高能量軌道激發所形成的組態．在用CI方法求解波函式時，在逐步增加組態的過程中如果能級前後的誤差小於10-5時，就認為CI已滿足精度要求，就不再增加組態了。
事實上，Debye模型並不需要高溫條件，只要r值足夠大，溫度不需要太高，體系也滿足Debye近似。但是，當電漿環境不滿足Debve近似時，電漿禁止效應就需要其他的模型來引入，比如離子球模型。幸運的是，一般的高溫電漿都滿足此條件。在上面的推導中，只引入了靜態禁止效應，而忽略了動態禁止效應。若要更精確地計算電漿禁止效應對原子結構的影響，就要把上面的各個因素都考慮進來。
