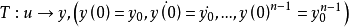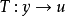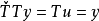非線性時變系統（Nonlinear time-varying systems）即同時滿足非線性系統和時變系統特徵的系統，它滿足其輸出不與其輸入成正比的特點，同時，當系統中某個參數值隨時間而變化時，整個特性也隨時間而變化。非線性時變系統的主要表示方式有狀態方程和結構圖，它的主要特徵有能控性、能觀性和穩定性分析。
基本介紹
- 中文名：非線性時變系統
- 外文名：Nonlinear time-varying systems
- 涉及學科：信息科學
- 特點：非線性和時變
- 對應：線性或時變
- 表示方式有：狀態方程和結構圖
非線性系統,簡介,分類,線性與非線性的意義與區別,時變系統,簡介,特點,分析,非線性時變系統特點,穩定性分析複雜,可能存在自激振盪,頻率回響發生畸變,非線性時變系統分析方法,描述函式法,逆系統法,
非線性系統
簡介
非線性系統是指一個系統,如果其輸出不與其輸入成正比，則它是非線性的。從數學上看，非線性系統的特徵是疊加原理不再成立。疊加原理是指描述系統的方程的兩個解之和仍為其解。疊加原理可以通過兩種方式失效。其一，方程本身是非線性的。其二,方程本身雖然是線性的,但邊界是未知的或運動的。
分類
非本質非線性：能夠用小偏差線性化方法進行線性化處理的非線性。
本質非線性：用小偏差線性化方法不能解決的非線性。
線性與非線性的意義與區別
意義
“線性”與“非線性”是兩個數學名詞。所謂“線性”是指兩個量之間所存在的正比關係。若在直角坐標系上畫出來，則是一條直線。由線性函式關係描述的系統叫線性系統。線上性系統中，部分之和等於整體。描述線性系統的方程遵從疊加原理，即方程的不同解加起來仍然是原方程的解。這是線性系統最本質的特徵之一。“非線性”是指兩個量之間的關係不是“直線”關係，在直角坐標系中呈一條曲線。最簡單的非線性函式是一元二次方程即拋物線方程。簡單地說，一切不是一次的函式關係，如一切高於一次方的多項式函式關係，都是非線性的。由非線性函式關係描述的系統稱為非線性系統。
區別
定性地說，線性關係只有一種，而非線性關係則千變萬化，不勝枚舉。線性是非線性的特例，它是簡單的比例關係，各部分的貢獻是相互獨立的；而非線性是對這種簡單關係的偏離，各部分之間彼此影響，發生耦合作用，這是產生非線性問題的複雜性和多樣性的根本原因。正因為如此，非線性系統中各種因素的獨立性就喪失了：整體不等於部分之和，疊加原理失效，非線性方程的兩個解之和不再是原方程的解。因此，對於非線性問題只能具體問題具體分析。
線性與非線性現象的區別一般還有以下特徵：
（1）在運動形式上，線性現象一般表現為時空中的平滑運動，並可用性能良好的函式關係表示，而非線性現象則表現為從規則運動向不規則運動的轉化和躍變；
（2）線性系統對外界影響的回響平緩、光滑，而非線性系統中參數的極微小變動，在一些關節點上，可以引起系統運動形式的定性改變。在自然界和人類社會中大量存在的相互作用都是非線性的，線性作用只不過是非線性作用在一定條件下的近似。
時變系統
簡介
時變系統(time-varying system)其中一或一個以上的參數值隨時間而變化，從而整個特性也隨時間而變化的系統。時變系統的特點是，其輸出回響的波形不僅同輸入波形有關，而且也同輸入信號加入的時刻有關。
特點
分析
在工程中，套用最廣的是所謂凍結係數法，這一方法的實質是在系統工作時間內，分段將時變參數“凍結”為常值，從而可分段地把系統看成為定常系統進行研究。通常，凍結參數法只對參數變化比較緩慢的時變系統才有效。對時變系統控制的一個可能的方案是，在採用估計器對參數進行線上估計的同時，採用適應控制系統實現控制。
非線性時變系統特點
非線性時變系統即同時滿足非線性系統和時變系統特徵的系統，它滿足系統其輸出不與其輸入成正比的特點，同時，當系統中某個參數值隨時間而變化時，整個特性也隨時間而變化。
穩定性分析複雜
在無外作用且系統輸出的各階倒數等於零時.系統處於平衡狀態。顯然，對於線性系統只有一個平衡狀態；而對於非線性系統，則可能存在多個平衡狀態，有穩定的平衡狀態和不穩定的平衡狀態，需要具體分析。
可能存在自激振盪
自激振盪是指沒有外界周期變換信號的作用時，系統內產生的具有固定振幅和頻率的穩定周期運動簡稱自振.
線性系統不可能形成穩定的自激振盪，而非線性系統在滿足一定條件下可能形成穩定的自振。
頻率回響發生畸變
非線性時變系統分析方法
描述函式法
在正弦輸入信號作用下，非線性時變系統的穩態輸出中一次諧波分量和輸人信號的複數比為非線性環節的描述函式，用N(A)表示，即
逆系統法
逆系統
所謂系統相當於對象在給定初始條件下。輸入到輸出的一個變換，即
n為系統階次。y為n階可微函式。
若在滿足初始條件的情況下，存在一個系統即變化
，
則稱該系統為原系統的逆系統。即有:
偽線性系統
將n階積分逆系統和原系統相串聯成複合系統，稱為偽線性系統。
線性控制的逆系統沒計方法
①狀態反饋控制。
②漸進跟蹤控制。
