基本介紹
- 中文名:集合論模型
- 外文名:model of set theory
- 別名:集理論模型
- 概念範疇:語義記憶
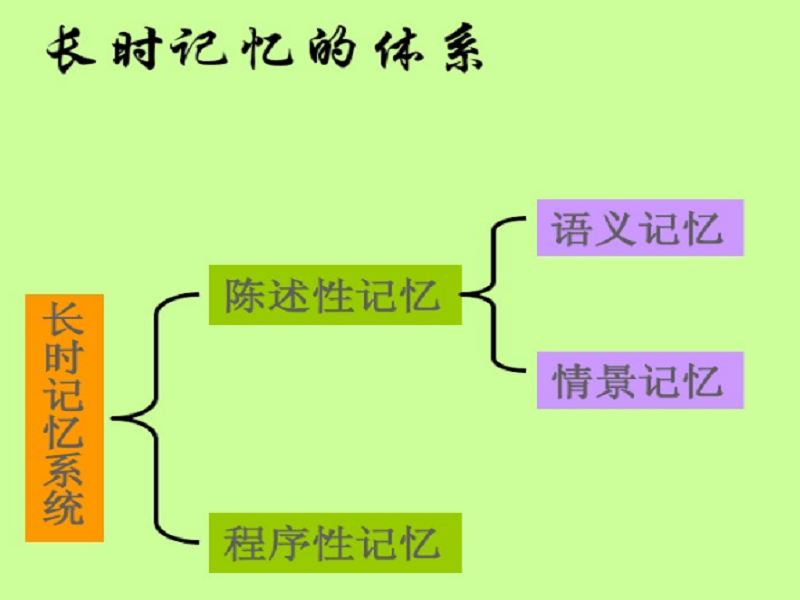
集合論模型,又叫集理論模型,該模型由Meyer提出,是長時記憶中的語義記憶的一種理論模型,它用要素集合的方式來解釋語義記憶的表征方式。定義集合論模型由Meyer提出,認為概念為語義記憶的單元。每一個概念都由集信息和要素來...
集合模型(set model)一類集合論語言模型.在集合論相容性與獨立性證明中,集合模型通常指域為集合的標準模型.由反射原理,對任何ZFC系統有限條公理而言,一定存在一個滿足這有限條公理的集合模型(參見“反射原理”).設B為強不可達基數,...
內模型法是從已知的一個模型M出發,來定義M的一個子模型 ,使得 滿足ZF的一些公理或者ZF以外的一些公理。公理集合論的一個著名成果就是1938年K.哥德爾所給出的 的證明,證明中用的就是內模型法,但是當時尚未如此命名。迄至1951年J...
《集合論模型中的大基數與組合性質》是依託中國科學院數學與系統科學研究院,由吳劉臻擔任項目負責人的青年科學基金項目。項目摘要 經由相容性和獨立性論證,不同集合論模型中的大基數性質和組合性質具有不同的特點。對這些大基數影響下的...
在公理集合論的研究中,大量的工作是關於集合論模型的,此外,還繼續此前樸素集合論對無窮組合問題的研究即組合集合論的研究。其中的一些問題是來源於柯尼希樹引理和 F. P.拉姆齊定理的推廣。另一分支則為描述集合論(亦稱解析集合論)...
所以 Zermelo 集合論的相容性是 ZFC 集合論的一個定理。Zermelo 的公理不允許很多無限基數的存在;例如,在 Zermelo 集合論的模型 Vω+ω 中對於有限序數 α 只有無限基數 。無窮公理現在通常被修改為斷言第一個無限馮·諾伊曼序數 的...
《集合論含有原子的自然模型和布爾值模型》是2011年北京師範大學出版社出版的圖書,作者是李娜。內容簡介 《集合論含有原子的自然模型和布爾值模型》由李娜所著,不僅從理論上豐富了數理邏輯的重要分支——公理集合論的刻畫集論模型的理論...
力迫推理也更易於操作.從科恩對連續統假設獨立性的證明過程可以看出,要想設計一個集合論模型滿足ZFC + }CH,構造一個比V小的模型是不可行的(參見“內模型法”),必須對V進行擴充,而V已經包括了所有集合,因此,從直觀上講,在ZFC...
布爾(Boolean)模型是基於集合論和布爾代數的一種簡單檢索模型。它的特點是查找那些與某個查詢詞返回為“真”的文檔。在該模型中,一個查詢詞就是一個布爾表達式,包括關鍵字以及邏輯運算符。通過布爾表達式,可以表達用戶希望文檔所具有...
內集合論的公理,即ZFC的公理加上(T),(S),(I),正好是非準分析的飽和模型中內集的基本性質。這也正是內集合論名稱的由來。套用 若令B(x,y)表示實數集合上的二元關係:x0,則(I)的左端顯然為真,即對任意標準的有限實數集z...
標準模型假設(standard model hypothesis)一種中間假設.它是美國數學家科恩(Cohen,P.J.)在介紹力迫法時引人的一個命題.在證明集合論外加公理的相容性時,通常以ZF公理系統本身的相容性作為前提.由模型論中的完備性定理,既然ZF系統...
兼納模型定理(generic model theorem)是關於力迫法的重要命題,該命題為證明集合論外加公理的相容性與獨立性提供了一個統計—模式。兼納模型定理(generic model theorem)關於力迫法的重要命題.它給出了兼納擴充的存在性條件.設M為ZF<...
可傳模型(transitive model)是一類標準模型。定義 若M為集合論語言的一個標準模型且M可傳,則稱M為一個可傳模型.可傳模型是集合論相容性與獨立性證明中最常採用的一類模型.模型的可傳性可保證模型滿足外延公理,也可保證許多集合論...
它是Zermelo集合論的模型。如果κ是不可及基數,則Vκ是Zermelo-Fraenkel集合論自身的模型,而Vκ+1是Morse–Kelley集合論的模型。注意所有個體階段Vα都是集合,但是它們的並集V是真類。在V中的集合叫做繼承良基集合;基礎公理要求所有...
公理1~5可以限制新集合形成的可能,從而消除羅素悖論中的集合(存在集合A滿足A不包含於自己)。公理6,連同1~4,按照馮諾依曼的提出(根據皮亞諾公理系統對自然數的描述)可以建立自然書數集N₀的標準模型。公理7在建立分析學時並不使用...
Skolem 的工作意味著,所謂“集合論(因此包含了幾何、算術,和其他使用集合論模型的理論)的絕對公理化”,似乎根本就不存在。(馮·諾伊曼)關於悖論的書卷仍未合上,而關於它的意義和可能的解決方案,亦未達成一致意見。(Abraham ...
如今,研究滿足很強的大基數假設又具有某種覆蓋性質的內模型,成了現代集合論中最富挑戰性和最深刻的課題.理論 可構造性(constructibility)一種可構造集理論.是研究集合的可構造性以及可構造集合的各種特殊性質的理論,也是證明集合論命題...
集合論模型與模型論中定義的模型有著非常密切的關係。一方面集合論模型只是對集合論語言的解釋,因此,它是一種特定語言的模型;另一方面模型論中的模型之論域必須為一集合,而集合論模型的域可以為一真類。儘管兩者有一定區別,但模型論...
但策梅洛集合論對進一步發展公理集合論和數學基礎中的其他工作,特別是模型論,是不夠的。 舉一個戲劇性的例子:上述超結構的描述並不能獨立地在策梅洛集合論中完成! 最後一步,構造 S成為一個無限並集,需要代換公理;這條公理在1...
,如此類推,對於任何標準的自然數k有{\displaystyle (n-k-1)\in (n-k)}。所以這是個無限遞降的元素序列。但是這個序列在這個模型中是不可定義的,因此它並不是集合,也就沒有違反正則公理。假定選擇公理 設非空集合S是正則公理...
布爾代數在代數學(代數結構)、邏輯演算、集合論、拓撲空間理論、測度論、機率論、泛函分析等數學分支中均有套用;1967年後,在數理邏輯的分支之一的公理化集合論以及模型論的理論研究中,也起著一定的作用。近幾十年來,布爾代數在自動...
。所以這是個無限遞降的元素序列。但是這個序列在這個模型中是不可定義的,因此它並不是集合,也就沒有違反正則公理。假定選擇公理,則"無限遞減的集合序列不存在"蘊涵正則公理 設非空集合S是正則公理的一個反例;就是說S的所有元素都...
如果T是一個範疇理論,則T只可能有有限模型,範疇理論必為完全理論。基數 亦稱勢。公理集合論的基本概念之一。是度量集合大小的量。在德國數學家康托爾(Cantor,G.(F.P.))之前,無窮只是一個很模糊的概念,人們無法區分兩個無窮集的...
在公理集合論(見集合論)中,用力迫法可以證明很多集合論命題的和諧性、獨立性,而在套用力迫法構作各種集合論模型時,為了方便,一般都是從一組集合論公理的一個可數模型出發。這種可數模型的存在性,就是在該組公理“有模型存在”...
其實,空集公理通常在無窮公理中被重複了,後者構造了一個集合,其中有一元素為空集。但是,有些公理化中,無窮公理所構造的集合併不被要求包含空集(例如包含一個任意元素),此時空集公理是必要的。有時可能要研究有限的集合模型,這時...
而利用ZF系統中的公理①~⑥及⑧、⑨(見集合論)雖然可以定義一個個具體的自然數,也可以定義自然數概念,但卻無法證明全體自然數的集合w={0,1,… }存在,也無法證明任何一個無窮集合的存在性。實際上,如果ZF(有模型,則全體繼承...
