基本介紹
- 中文名:空集公理
- 外文名:axiom of empty set
- 套用學科:數學
- 套用領域:集合論
- 相關術語:替換公理模式
- 屬於:Zermelo-Fraenkel 集合論
形式陳述
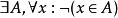
解釋
- 存在一個空集。

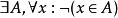
在集合論中,空集公理是 Zermelo-Fraenkel 集合論的公理之一。常常用它和替換公理模式證明分離公理模式(證明需要排中律),而不把後者當作一條公理。後者和“至少存在...
空集是指不含任何元素的集合。空集是任何集合的子集,是任何非空集合的真子集。空集不是無;它是內部沒有元素的集合。可以將集合想像成一個裝有元素的袋子,而...
初等集公理是集合論的一條公理,策梅洛(E.F.F.Zermelo)於1908年提出集合論公理體系時,其中有一公理稱為初等集公理,該公理斷言:存在空集,它不含任何元素;如果a...
第一個常用的公理系統是策梅洛和弗倫克爾等提出的Z-F集合論公理系統。這個系統中只有一個非邏輯二元關係符號“∈”,非邏輯公理有:外延公理、空集公理、無序對...
子集公理模式的提出,是為了對集合的規模加以限制,即把集合論的創始人G.F.P.康托爾所認為的滿足一個性質的全體對象組成一個集合,這樣一種概括過程限制在一個已...
參見空集公理、對集公理。公理III。分離公理 (Axiom der Aussonderung):“只要命題函式 –(x) 對於一個集合 M 的所有元素是明確的,則 M 擁有一個子集 M' ...
基數亦稱勢。公理集合論的基本概念之一。是度量集合大小的量。在德國數學家康托爾(Cantor,G.(F.P.))之前,無窮只是一個很模糊的概念,人們無法區分兩個無窮集...
策梅洛的主要貢獻是集合論基礎,1904年發表的論文不僅解決了G.康托爾的良序問題,而且給出了選擇公理(也稱為策梅洛公理),它有上百種等價形式,已套用於幾乎每一...
在公理集合論中,單元素集合的存在性是空集公理和配對公理的結果:前者產生了空集Ø,後者套用於對集 Ø 和 Ø,產生了單元素集合 {Ø}。...
,是一個沒有任何元素的集合,因為集合可完全由其元素來確認,因此只有一個空集合(參考空集公理)。雖然空集合沒有任何元素,但空集合本身可以是其他集合的元素。因此...
例如,在策梅洛(Zermelo)和弗倫克爾(Fraenkel)等提出的ZF公理系統(也稱ZFC公理系統)中,嚴格規定了一個集合存在的條件(簡單地說,存在一個空集【空集公理】;每個...
3.4 一階謂詞邏輯公理系統3.5 一階謂詞邏輯自然推理系統3.6 一階謂詞邏輯系統元理論第四章 公理集合論基礎4.1 ZFC簡介4.2 外延公理、空集公理和子集公理...
在公理集合論中,單元素集合的存在性是空集公理和對集公理的結果:前者產生了空集{},後者套用於對集 {} 和 {},產生了單元素集合 {{}}。...
它的非邏輯公理有:外延公理、空集公理、無序對公理、並集公理、冪集公理、替換公理模式、正則公理。如果另加選擇公理( )則所得到的公理系統簡記 。...
它的非邏輯公理有:外延公理、空集公理、無序對公理、並集公理、冪集公理、替換公理模式、正則公理。如果另加選擇公理(AC),則所得到的公理系統簡記為ZFC。...
