基本介紹
- 中文名:
- 外文名:
- 所屬學科:
- 所屬問題:
- 簡介:
- 提出者:
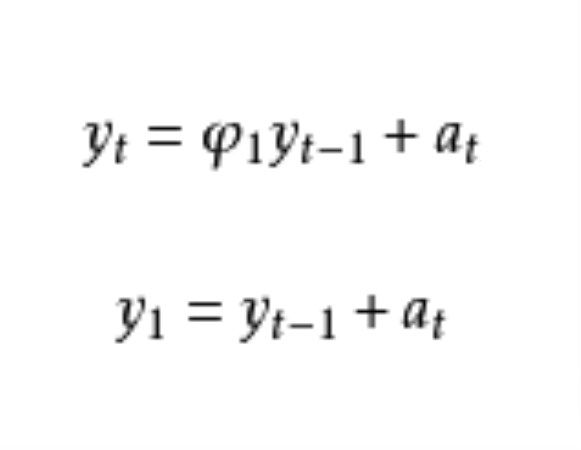
若時間序列{xt}適合於模型xt+xt-1=εt,其中{εt}是均值為零,方差為σε²的白噪聲序列,則稱其為隨機遊動模型。隨機遊動是一階自回歸模型[AR (1)]參數為a=1的極端情形。這時 {xt}不具有平穩性, 因為...
隨機遊走(random walk)也稱隨機漫步,隨機行走等是指基於過去的表現,無法預測將來的發展步驟和方向。核心概念是指任何無規則行走者所帶的守恆量都各自對應著一個擴散運輸定律,接近於布朗運動,是布朗運動理想的數學狀態,現階段主要套用...
隨機環境中的隨機遊動 [random walk in random environments]設(V,E)是無窮的有向圖,具有可數的頂點集 V 和邊集 。對任意 ,定義它的鄰域(neighborhood),表示支撐為 的 V 上的機率測度全體。中的元素稱為在 v 點的轉移律(...
《多型分枝隨機遊動在依時隨機環境中的漸近性質》是依託北京工商大學,由梁新剛擔任項目負責人的青年科學基金項目。項目摘要 多型分枝隨機遊動是經典的分枝隨機遊動的推廣,是研究多物種種群性質和遷移的一個主要模型,是機率論和隨機過程...
本項目主要研究經典的分支隨機遊動的一些推廣和一些現有結果的更深入的探索。其中擬解決的問題都是基於最近幾年來申請者和其他研究者在分支隨機遊動及其相關模型上取得的一些新的研究進展,具體分為以下四個方向: 1.基於已知的幾類特殊...
對Poisson幾何小世界模型和修正的Newman-Watts模型,我們分別研究其上的隨機遊動,我們證明它們是快速混合的,即過程以極快(相比於網路規模)的速度達到平穩分布。另一方面,對經典的小世界網路,隨機圖模型,我們研究其上的尾達滲流。
《隨機環境中隨機遊動與分枝系統》是依託長沙理工大學,由李應求擔任項目負責人的面上項目。項目摘要 本項目研究隨機環境中依賴年齡分枝過程矩的有限性;引入隨機環境中隨機指標分枝過程並研究該模型矩的性質.研究隨機環境中兩性分枝過程的性質...
依時隨機環境中的分枝隨機遊動的模型提煉自具體生物和生態學實例,如植物繁衍、細胞老化和寄生蟲感染等,具有廣泛的套用價值。在本項目中,我們著重考慮依時隨機環境中在d維實數空間中取值的分枝隨機遊動,主要研究關於其中第n代個體的...
本書把流體看作若干個質點所組成的質點系,以研究個別流體質點的運動為基礎,在室內水槽試驗的基礎上,建立分層分條帶水流模型、加權自動迎風格式隨機遊動模型和質點追蹤法模型,給出典型算例,並對河流、水庫、潮汐渠道與電站引水渠道、...
而CLWD結構是我們首次提出的一個隨機變數的新的相依結構,它包含了很多常見的相依隨機變數。特別地,非常有名的n元Samarnov分布服從這個相依結構。我們在這個結構下,將所得的隨機加權和及其最大值的尾漸近性結果套用到風險模型中,給出...
第七章介紹了Brown運動的概念和部分基礎性質,它是重要的隨機模型,與其他數學分支及物理學、生物學、金融學都有著深刻的聯繫,以它作為該書的結束,希望讀者對於隨機過程的理論和套用價值有一個更深刻的認識。圖書目錄 章 機率論述要…...
幾何Brown運動 7.6.5 有漂移的Brown運動 習題七 第8章 隨機積分 8.1 關於隨機遊動的積分 8.2 關於Brown運動的積分 8.3 Ito積分過程 8.4 Ito公式 8.5 隨機微分方程 8.6 Black-Scholes模型 習題八 習題參考答案 參考文獻 ...
設在某一時刻容器A中恰有.i個分子,在下一次試驗中,系統的可能狀態是i-1或i+1,這要看分子是從A中選出還是從B中選出而定,相應的機率是j/N和(N-j>/N).這樣的試驗可用如下稱為愛倫弗斯特模型的隨機遊動來描述:質點運動的...
正如已經指出的,河流剖面可以用隨機遊動模型來近似模擬,在模型中隨機遊動的步子是限於要么向下要么在水平向外。從填圖的觀點來看,隨機遊動方法也可以用來模擬水網的發育過程。在這兒限制有點不同。而且在隨機遊動中理所當然的“爬山...
隨機性的否定 提取有效信號的方法。a、簡單隨機遊動 簡單隨機遊動可作為許多客觀現象的模型,並且顯示出不同程度的近似真實性。公式:sn(+1,-1)=x1+x2+…+xn 其中x1,x2,…,xn是整數集i=?+1,-1?中以固定機率出現的、...
這部分研既能促進連續時間隨機遊動模型在各領域的套用,還為分數偏微分方程的解提供一種機率逼近方法,也有助於了解抽象測度穩定過程和具有各向異性的穩定隨機場的構造.二是研究穩定過程的機率與幾何性質.重點是研究自相似穩定過程的漸進...
馬爾可夫過程(Markov process)是一類隨機過程。它的原始模型馬爾可夫鏈,由俄國數學家A.A.馬爾可夫於1907年提出。馬爾可夫過程是研究離散事件動態系統狀態空間的重要方法,它的數學基礎是隨機過程理論。概念 1.馬爾可夫性:設 為一隨機...
