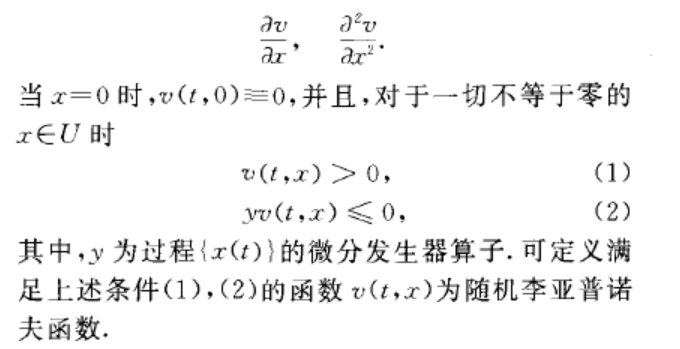
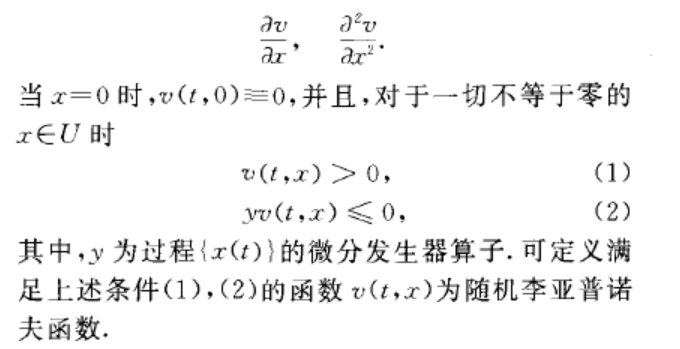
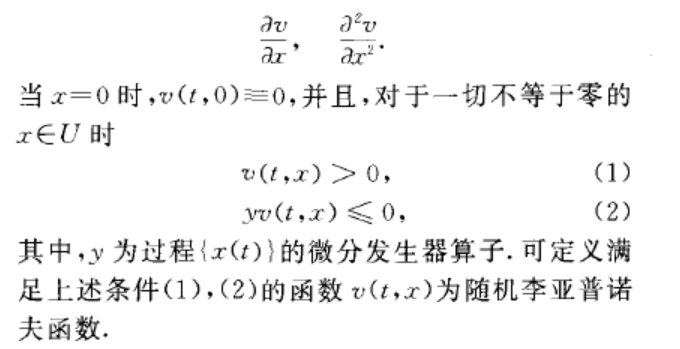
隨機李亞普諾夫函式(stochastic I,iapunovfunction)研究隨機動態系統漸近性質的工具.它是幫助人們在不求解隨機微分方程的情況下,定性地研究該隨機系統的漸近性態.例如,隨機穩定性、各態歷經性、循環、瞬態、平穩性等,這些概念都是用於...
穩定性的函式V(x)被稱為李亞普諾夫函式.有興趣的讀者,建議參考相關的專業書籍,參考資料中筆者列出的兩本著作,適合從初學者到從業者各個認知度的讀者參閱。Let x = 0 be an equilibrium point for x = f(x)and D : Rn b...
李亞普諾夫方程,或稱李亞普諾夫矩陣方程,是指對於沒有外部輸入的線性定常連續系統,用以構造李亞普諾夫函式的方程,或使系統原點平衡狀態漸進穩定的充分必要條件。其形式為見正文。基本概念 李亞普諾夫穩定性 在1892年,俄國數學家李亞...
李亞普諾夫函式法(method of I,iapunov func-dons)研究概周期解存在性的一種方法.用李亞普諾夫函式法討論概周期解的存在性問題通常有兩個途徑,或保證緊集KCR”中有界解的惟一性或確定有界解的某種穩定性質,從而分別藉阿梅留定理或...
向量李亞普諾夫函式(vector Liapunov func- tion )由大系統之各個子系統的李亞普諾夫函式構成的向量函式.它可用來判別大系統的穩定性.向量李亞普諾夫函式由美國數學家貝爾曼((Bellman , R.)於1962年提出,後於1966年由拜利(Bailey , F...
李亞普諾夫函式分解法(decomposition meth-od by I,iapunov function)大系統穩定性分解的一種方法.其一般步驟為:1.將大系統分解為若干子系統,使得可找出各孤立子系統的李亞普諾夫函式,並用它分析各孤立子系統的穩定性.2.研究子系統...
李亞普諾夫泛函方法是李亞普諾夫第二方法對泛函微分方程的一種推廣。背景 用李亞普諾夫函式V(t,x)研究RFDE(f):ẋ(t)=f(t,x)的穩定性,因為有了拉茲密辛條件而大大擴展了套用範圍,然而仍有很大的局限性,而且無法證明V函式的...
其中 P(t) 在 t≥τ 上連續,李亞普諾夫引進了一些數,現在稱之為李亞普諾夫特徵數,來代替特徵根的作用,它們是用來測定 時其解的“指數”增長的數。具體內容 李亞普諾夫特徵數,設φ(t) 是定義與t≥τ 上的實函式,則 為...
在機率論方面,李雅普諾夫引入了特徵函式這一有力工具,從一個全新的角度去考察中心極限定理,在相當寬的條件下證明了中心極限定理,特徵函式的引入實現了數學方法上的革命。歷史 這一穩定性以俄國數學家亞歷山大·李亞普諾夫命名,他在...
李亞普諾夫第二方法就是藉助於一個所謂李亞普諾夫函式V(x,t)及根據微分方程所計算得到的V沿著軌線的導數dV/dt的符號性質來直接推斷穩定性問題。簡介 李亞普諾夫第二方法是通過尋找滿足某種幾何性質的函式值直接推證方程組穩定性的一種...
李亞普諾夫曲面(Liapunov surface),指的是體積分及曲面積分相互轉化的格林公式對任意連續可微函式都成立的一類區域的邊界曲面。R”中的區域日的邊界S如果滿足下列條件,則稱S為李亞普諾夫曲面: 1.S被有限個n維區域覆蓋,在每個區域內的...
1892年在博士論文《運動穩定性的一般問題》中,開創性地提出求解非線性常微分方程的李亞普諾夫函式法,亦稱直接法,它把解的穩定性與否同具有特殊性質的函式(通常稱為李亞普諾夫函式)的存在性聯繫起來,這個函式沿著軌線關於時間的導數...
它包括離散和連續兩種模型.離散霍普菲爾德模型是一種離散時間網路,它由n個神經元構成.S取值為1或一1,神經元隨機、異步地按下述規則改變狀態:對於W,} - W},的對稱網際網路,引人能量函式 (李亞普諾夫函式)則網路演變過程E是單調...
檢查有沒有類似守恆量的耗散量(見李亞普諾夫函式)。利用泰勒展開式作線性近似。利用變數變換法,改寫成較易分析的方程。分岔理論。微擾法(也可套用在代數方程上)。偏微分方程 參見:非線性偏微分方程列表 研究非線性偏微分方程最常見...
它由帕塞瓦爾(Parseval,C.M.-A.)於1805年提出但未證明。對於黎曼可積函式情形是李亞普諾夫(Ляпунов,А.М.)於1896年證明的。1906年,勒貝格(Lebesgue,H.L.)對於勒貝格平方可積函式給出證明。人物簡介 Marc-Antoine ...
4.4.1 二次型函式及其定號性 4.4.2 李亞普諾夫第二法 4.5 線性定常系統李亞普諾夫穩定性分析 4.5.1 李亞普諾夫第一法(間接法)4.5.2 李亞普諾夫第二法 4.6 線性時變系統李亞普諾夫函式的求法 4.6.1 線性...
李亞普諾夫函式是研究非線性控制問題的一個重要手段。切apunov方法可以分為第一方法和第二方法。Lyapunov第一方法主要原理是把非線性系統在其工作點附近進行線性化,然後利用線性系統理論對系統穩定性進行分析,但是,當被控系統工作點變化...
