基本介紹
- 中文名:阿基米德公理
- 外文名:archimedean axiom
- 別稱:阿基米德性質
- 命名者:奧地利數學家Otto Stolz
- 命名時間:1883年
- 套用學科:數學
描述
 阿基米德
阿基米德形式敘述
解釋
- 給出任何數,你總能夠挑選出一個整數大過原來的數。
- 給出任何正數,你總能夠挑選出一個整數其倒數小過原來的數。
與實數的關係

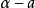

歷史
證明
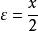
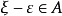





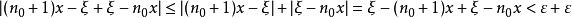
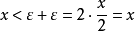

 阿基米德
阿基米德
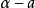

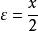
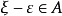





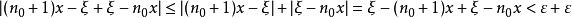
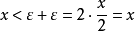
在抽象代數和分析學中,以古希臘數學家阿基米德命名的阿基米德公理(又稱阿基米德性質),是一些賦范的群、域和代數結構具有的一個性質。粗略地講,它是指沒有無窮大或...
的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂準則)中,並不是每一個都能推出阿基米德公理的...
阿基米德公理:對任意a,b∈R,a>0 存在正整數 n ,使 na>b 。(III)(2)完備性公理R中的任何基本列都在R中收斂。稱滿足公理組I的集為域;滿足公理組I與II...
阿基米德性質是阿基米德在其著作《論球與圓柱體》中明確的性質。...... 阿基米德性質是阿基米德在其著作《論球與圓柱體...(參見本卷《高等幾何》中的“阿基米德公理”...
阿基米德公理是線段度量的根據。阿基米德公理 在長短不同的兩條線段中,無論較長的線段怎樣長,較短的線段怎樣短,我們總可以在較長的線段上連續截取較短的線段,並且...
度量幾何即歐幾里得幾何,是確定或表述幾何量中長度、面積和體積的一種方法。最早人們依靠直觀進行推演計算。歐幾里得《幾何原本》中套用的“阿基米德公理”成為近代幾何...
給出的一些數學的基本“定義”,如在端點相同的所有線(包括曲線、直線)中,以直線為最短、對於任意二正實數 a,b,必存在自然數n,使得na>b(著名的阿基米德公理),...
(2)直線完備公理(axiom of linear completeness)一直線上所有滿足結合公理、順序公理、契約公理和阿基米德公理的點的集合不可能擴充成仍然滿足這些公理的更大的集合。...
論球與圓柱,這是古希臘數學家阿基米德的力作。給出的一些數學的基本“定義”,如在端點相同的所有線(包括曲線、直線)中,以直線為最短、對於任意二正實數 a,b,...
