基本介紹
- 中文名:阿基米德公理
- 外文名:archimedean axiom
- 別稱:阿基米德性質
- 命名者:奧地利數學家Otto Stolz
- 命名時間:1883年
- 套用學科:數學
描述
 阿基米德
阿基米德形式敘述
解釋
- 給出任何數,你總能夠挑選出一個整數大過原來的數。
- 給出任何正數,你總能夠挑選出一個整數其倒數小過原來的數。
與實數的關係

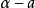

歷史
證明
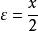
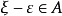





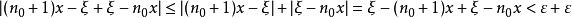
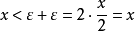

阿基米德性質一般指本詞條
 阿基米德
阿基米德
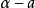

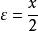
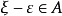





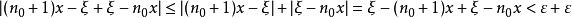
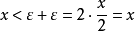
阿基米德性質是阿基米德在其著作《論球與圓柱體》中明確的性質。...... 阿基米德性質是阿基米德在其著作《論球與圓柱體》中明確的性質。目錄 1 定義 2 形式 ...
在抽象代數和分析學中,以古希臘數學家阿基米德命名的阿基米德公理(又稱阿基米德性質),是一些賦范的群、域和代數結構具有的一個性質。粗略地講,它是指沒有無窮大或...
阿基米德螺線(亦稱等速螺線),得名於公元前三世紀希臘數學家阿基米德。阿基米德螺線是一個點勻速離開一個固定點的同時又以固定的角速度繞該固定點轉動而產生的軌跡...
上面推出的幾個性質,有的前人已證明,有的阿基米德在別處已證明,在這裡是作為已知條件來使用的.例如:1)過D且平行於軸的直線必過弓形的頂點B,且B是ED中點,在...
阿基米德(公元前287年—公元前212年),偉大的古希臘哲學家、百科式科學家、數學家、物理學家、力學家,靜態力學和流體靜力學的奠基人,並且享有“力學之父”的美稱,...
設E是實數域上的矢量空間,若向量格V作為格群是阿基米德格群,則稱V是阿基米德向量格。...
非阿基米德賦值(non-archimedian norm)是局部域上的一種特殊映射。...... 局部域可粗分為兩類:一種的絕對值滿足阿基米德性質(稱作阿基米德局部域),另一種的絕對值...
阿基米德半群(Archimedean semigroup)是單半群的一種推廣。半群S,若對任意a,b∈S,存在n使得a∈SbS(a∈Sb,a∈bS,a∈bS∩Sb),則稱S為阿基米德的(左阿基米德...
阿基米德·莫爾萊奧(Archimede Morleo),1983年9月26日出生於義大利梅薩涅(Mesagne,Italy),義大利職業足球運動員,司職左後衛,效力於義大利足球乙級聯賽巴里足球俱樂部。....
子域上阿基米德序域(Archimedean orderedfield over a subfield)是一類相對於子域具有特殊性質的序域。...
北京阿基米德智慧型門窗有限公司於2002年10月22日成立。法定代表人魏方紅,公司經營範圍包括:銷售建築材料(不含砂石及砂石製品)、不鏽鋼製品、五金;貨物進出口、技術進...
阿基米德·莫萊奧,在萊切開始職業生涯,2002-03賽季被租借至卡拉雷瑟、次季租借至索拉,賽季末被買斷,但2004-05賽季結束後索拉俱樂部破產。2007年8月,莫萊奧加盟...
廣西阿基米德體育文化發展有限公司於2017年06月16日成立。法定代表人韓毅,公司經營範圍包括:對體育文化業的投資,體育、文化活動的組織、策劃;體育場館服務(除前置許可...
實數具有阿基米德性質(Archimedean property),即 , ,若 ,則∃正整數 , 。實數稠密性 實數集具有稠密性,即兩個不相等的實數之間必有另一個實數,既有有理數,...
(III)(1) 阿基米德公理(也稱阿基米德性質,它並不是嚴格意義上的公理,可以由完備性公理證明。在歐幾里得的幾何書中,它僅被描述為一個命題)。...
螺線(Spiral),也稱定傾曲線,指任何一種圍繞一個中心點或一條軸旋轉,同時又逐漸遠離的動點的軌跡。例如螺旋線(非平面曲線)及常用的平面螺線、阿基米德螺線、對數...
簡介《引理集》 阿基米德著作之一 只有阿拉伯文譯本傳下來,是15個初等幾何的問題集.也許不是阿基米德的原著而是後人收集整理的,因為在文章中不止一次提到阿基米德的...
《論浮體》 作者:【古希臘】 阿基米德...... 《論浮體》 作者:【古希臘】 阿基米德 中文名 論浮體 作者 阿基米德 性質 第一部流體靜力學著作 相關 在推理...
