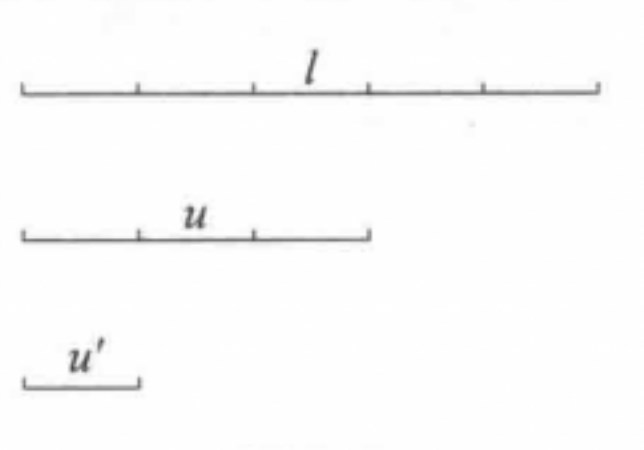
有公度線段(commensurable line segments)亦稱可通約線段或稱可公度線段，是平面幾何的基本概念之一，指有公度的兩線段。對於線段u和線段a、b，如果用線段u去量a，m次剛好量完，不多也不少；同樣，用u去量b，也剛好量n次量完。這時我們說，線段a和b是可公度的，而線段u稱為線段a和b的公度。
基本介紹
- 中文名：有公度線段
- 外文名：commensurable line segments
- 所屬學科：數學（平面幾何）
- 別稱：可通約線段或可公度線段
- 簡介：有公度的兩線段
基本介紹,線段度量的根據,求兩線段最大公度,
基本介紹
兩條線段如果各含有第三條線段的整數倍而沒有剩餘，那么第三條線段就叫做這兩條線段的公度。
例如，線段a、b、u(a、 b>u)，用u去量a得整數m倍，量b得整數n倍，都沒有剩餘，也就是說，線段a、b都可以分別用線段u的m倍和n倍來表示，即a=mu，b=nu，我們就說線段u是線段a、6的公度，線段a、b就叫做有公度線段。
如果線段u是線段a、b的公度，那么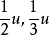
、.....也必然是a、b的公度。因此，兩條線段如果有某一個公度， 它們就一定有無數個公度，而在這無數個公度中必定有一個最大的公度，但沒有最小的公度。
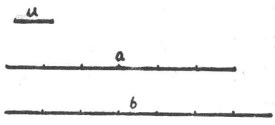圖1線段度量的根據
阿基米德公理是線段度量的根據。
阿基米德公理 在長短不同的兩條線段中，無論較長的線段怎樣長，較短的線段怎樣短，我們總可以在較長的線段上連續截取較短的線段，並且截到某一次以後，就得出下面兩種情形中的一種：或者沒有剩餘，或者得到一條短於較短線段的剩餘線段。
阿基米德（Archimedes，公元前287-212年）是希臘數學家，這個公理換句話說就是：已知兩條線段a和b，並且a>b，那么我們總可以求出一個整數m，使mb≤a，並且(m+1)b>a，就是使mb≤a<(m+1)b。
求兩線段最大公度
輾轉相解法求線段的最大公度
從下面的基本定理，我們就可以找到求兩條線段的最大公度的方法。為了敘述方便，用(a，b)表示線段a和b的最大公度。
定理設有兩線段a和b。
(1)如果a=b，那么(a，b)=a=b(圖2)；
(2)如果a>b，用b去量a剛好量m次量完，那么(a，b)=b(圖3)；
(3)如果a>b，用b去量a，量若干次後剩下一段線段c，而0<c<b，那么(a，b)=(b，c)(圖4)。
證明:
(1)、(2)是很明顯的。我們主要證明( 3 )。
首先，設u是b、c的公度，那么用u去量b和c，一定都剛好量完，所以也剛好量完a。因此，u一定是a、b的公度。反過來，設u是a、b的公度，那么用u去量a和b，一定都剛好量完。因此，用u去量c，也剛好量完。所以u一定也是b、c的公度。這就是說，a、b的公度和b、c的公度是完全一樣的。因此，a、b的最大公度和b、c的最大公度也相等。
根據這個定理，我們可以得到求兩線段最大公度的法則：
例如要求線段a和b的最大公度。設a>b，那么用圓規在a上從一個端點起連續截取等於b的線段。込祥截取若干次後，有兩種可能的結果：
(1)截取若干次後，剛好截完，這吋(a, b)=b；
(2)截取若干次後，剩下一段c，而0<c<b，這時求(a，b)就可以轉為求(b，c)。
要求(b，c)用上面相同的方法，在b上連續截取等於c的線段，截若干次後，也有兩種可能的結果：
圖5(1)截若干次後，剛好截完，這時(a，b)=(b，c)=C；
(2)截若干次後，剩下一段d，而0<d<c，這時求(b，c )又轉為求(c，d)。
繼續上面的步驟，每次都可能有上面的兩種結果。如果一旦出現第(1)種情形，那么就找到了最大公度。但是，如果永遠不會出現第(1)種情形，就是說，如果相互截取，永遠有餘量，這時我們就找不到a、b的最大公度，也找不到它們的公度。在這種情況下，我們說a、b是不可公度的。
從上面的討論可以知道，如果兩條線段是可公度的，那么用上面的方法一定可以找到它們的最大公度。這種方法叫做輾轉相截法，它和算術中用輾轉相除法求兩個自然數的最大公約數的方法相類似。
現在的問題是：不可公度的線段是否存在?下面的定理告訴我們，這樣的線段是存在的。
定理1等腰直角三角形的斜邊和直角邊是不可公度的。
定理2如果一條線段和長度單位是可公度的，那么這條線段的量數是有理數。
定理3如果一條線段的量數是有理數，那么這條線段和長度單位是可公度的。
從定理2知道，“一條線段和長度單位可公度”這個條件能保證“這條線段的量數是有理數”這個結論成立。足夠保證結論成立的條件叫做充分條件。從定理3又知道，如果“一條線段的量數是有理數"成立，那么非有“這條線段和長度單位可公度"這個條件不可，也就是說，這個條件是結論成立的必不可少的條件，叫做必要條件。既充分又必要的條件叫做充分必要條件，簡稱充要條件。但必須注意，使某一結論成立的充分條件不一定是必要條件，例如“兩個角是對頂角”是“這兩個角相等"的充分條件，但不是必要條件。同樣，必要條件也不一定是充分條件，例如“兩條對角線相等”是“一個四邊形是正方形”的必要條件，但不是充分條件。只有當一個定理的逆命題也成立時，這個定理中的條件才是結論成立的充要條件。利用充要條件這個概念，我們可以把上面的定理2和定理3合併起來，寫成：
定理4一條線段的量數是有理數的充要條件是：這條線段和長度單位是可公度的。
從這個定理知道，如果被測線段和長度單位是不可公度的線段，那么這條線段的量數一定是無理數。反過來也對。
