論球與圓柱,這是古希臘數學家阿基米德的力作。給出的一些數學的基本“定義”,如在端點相同的所有線(包括曲線、直線)中,以直線為最短、對於任意二正實數 a,b,必存在自然數n,使得na>b(著名的阿基米德公理),然後從這些“定義”出發,推導出全書上卷44個,下卷9個命題。本書是阿基米德的得意傑作,包括了數學域的許多重大成就.
基本介紹
- 書名:論球與圓柱
- 作者: 阿基米德
- 國家:古希臘
- 內容:定義、命題
產生背景,理論原理,一些例子,
產生背景
論球與圓柱是阿基米德的得意傑作,包括許多重大成就.序言是阿基米德給多西修斯(Dositheus)的信,後者是科農的學生和朋友.阿基米德的著作,過去一向是通過科農轉給亞歷山大的學者的.科農去世後,改由多西修斯代辦.在《拋物線圖形求積法》的序言中,阿基米德已經說明了這一點:“驚悉科農去世,我十分悲痛,這不僅僅因為失去一位好友,而且失去一位令人欽佩的數學家.你是他的朋友,而且精通幾何,轉交論文的任務,現在請你代勞”.以後好幾篇著作都是先寄給多西修斯的.

理論原理
在《論球與圓柱》的序言中,首先指出本篇的主要內容和成就,接著給出6個定義.阿基米德在這裡將“定義”說成“公理”.按其性質來說應該是定義,後來歐托基奧斯在注中說明這一點.
下面給5個假定,相當於公理.例如
1.在端點相同的所有線(包括曲線、直線)中,以直線為最短.
2.在以相同的平面曲線為邊界的曲面中,以平面的面積為最小.
特別重要的第5個公理,這就是後來以阿基米德的名字命名的公理:如果兩條線段或兩個面、兩個立體不相等,就可以在兩者之差的上面,加上它的本身,一次一次加上去,使得每一個預先給定的同類量都被超過.在現代分析學中常用的說法是:對於任意二正實數 a,b,必存在自然數n,使得na>b.
從這些定義和公理出發,推導出上卷44個,下卷9個命題.多次使用阿基米德公理及反證法(歸謬法),如要證A=B,則證明A>B及A<B均導致矛盾.
較為著名的命題有:
上卷:
命題14.正圓錐體的側面積等於以底面半徑與母線的比例中項為半徑的圓的面積
命題34.球體積等於以它的大圓為底、它的半徑為高的圓錐體積的4倍.推論:以球的大圓為底、球直徑為高的圓柱的體積與表面積分別是球的體積與表面積的3/2.這命題在《阿基米德方法》中已提出,此處用反證法加以證明.
命題35—44研究了球缺、球冠及球心角體(球扇形)的表面積及體積.
下卷:(9個命題主要討論球缺,好幾個是作圖題.)
命題2給出球缺的體積.
命題4在歷史上占有特殊的地位.它要求用平面將一個球截成兩部分,使這兩部分體積之比等於給定的比.
——此問題的解相當於用幾何方法去解這個3次方程.阿基米德說他將在後面給出分析與綜合的解法,但現存本未見,大概已失傳.後來歐托基奧斯(5世紀時)找到一些殘頁,是用多利安方言(阿基米德慣用的方言)寫的手稿,上有這問題的解法,他認為是屬於阿基米德的.
一些例子
(註:1、此處的黑體字都表示一個變數,2、注意此處的l都為小寫的L,i的大寫因與I相似,故各處的L與i都用大寫表示)
阿基米德引用了歐幾里得《幾何原本》Ⅻ,2的證法(窮竭法)建立了命題6:只要邊數足夠多,圓外切正多邊形的面積C與內接正多邊形的面積1之差可以任意小.不同之處是歐幾里得默認了阿基米德公理,而阿基米德在本篇中是明確地作為公理提出來的.在這基礎上,證明了:
命題14.正圓錐體的側面積等於以底面半徑與母線的比例中項為半徑的圓的面積.
設正圓錐的底面為A,半徑為r,母線為L,r與L的比例中項為 R(即R^2=r·L),則此正圓錐的側面積S=πR^2.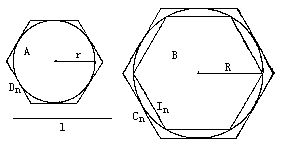

以R為半徑作圓B,其面積為πR^2,現要證明S=B=πR^2.用反證法,設S>B.根據命題6,可作B的外切正多邊形Cn(同時表示其面積,下同)與內接正邊形In,使得Cn:In<S:B
又作底面A的相同邊數的外切正多邊形Dn,其周長記作Pn.以Dn為底,以圓錐的頂點為頂點的正稜錐的側面積為Ln=1/2LPn
而,Dn=1/2rPn
Dn與Cn是相似的其比等於對應線段平方之比,
由此知Cn=Ln,代入上面的不等式有Cn:In=Ln:In<S:B

這是不合理的,因為圓錐側面積S小於其外切稜錐側面積Ln,而圓B大於其內接多邊形面積In.同理可證S<B也是不合理的,故S=B=πR^2.現在常用的形式是S=πrL.

