基本介紹
- 中文名:錯位相減法
- 外文名:Dislocation Subtraction
- 別稱:錯位法
- 表達式:1/[n(n+1)]=(1/n)- [1/(n+1)]
- 套用學科:數學
- 適用領域範圍:代數
- 適用領域範圍:數列
條件
舉例
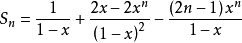
解題套用
典例1:

(2)當a≠1時,Sn=a+2a2+3a3+…+nan……①
①×a得,aSn= a2+2a3+3a4+……+nan+1 ……②
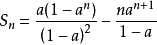
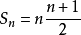

典例2:

典例3:

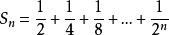

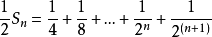


典例4:
公式的推導






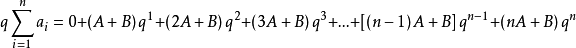





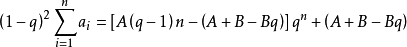

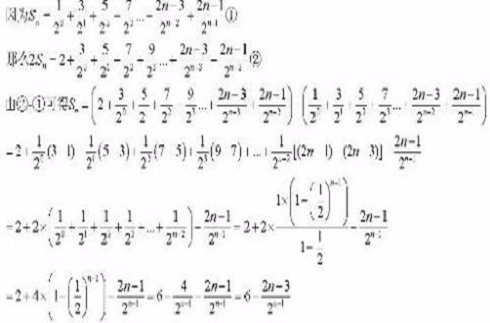
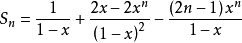

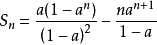
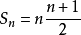



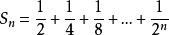

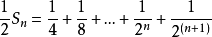








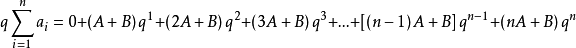





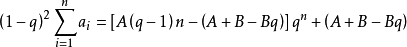

兩式相減得(1-x)Sn=1+2(x+x2+x3+x4+…+xn-1)-(2n-1)xn化簡得錯位相減法解題套用 編輯 錯位相減法是數列求和的一種解題方法。在題目的類型中:一般是...
數列求和的常用方法:公式法、裂項相消法、錯位相減法、倒序相加法等。關鍵是找數列的通項結構。28、分組法求數列的和:如an=2n+3n29、錯位相減法求和:如an=(...
數列求和對按照一定規律排列的數進行求和。求Sn實質上是求{Sn}的通項公式,應注意對其含義的理解。常見的方法有公式法、錯位相減法、倒序相加法、分組法、裂項法、...
[1] 差比數列的性質,就是由成倍遞增的一組數所組成的數列.求和公式,可用錯位相減法[2] 推出。差比數列公式 數列公式對稱公式 編輯 對稱數列的通項公式:...
1、分組法求數列的和:如an=2n+3n2、錯位相減法求和:如an=n·2^n3、裂項法求和:如an=1/n(n+1)4、倒序相加法求和:如an= n...
2、計算方法:先將各施工過程中的流水節拍時間相累加,然後將各相鄰施工過程的累加結果錯位相減,然後從相減結果中選出最大值,這個值便是兩相鄰施工過程同一施工段的...
1、分組法求數列的和: 如an=2n+3n ,an=2n+3n ,an=2n+3n2、錯位相減法求和:如an=n·2^n3、裂項法求和:如an=1/n(n+1)...
差比數列是由一個等差數列和一個等比數列相乘得到的新數列,其求和是高中數學常考內容。但學生在利用錯位相減法進行差比數列求和時,往往只能寫出前幾步,整理不出最終...
(9)利用裂項法進行放縮。(10)利用錯位相減法進行放縮。放縮法注意事項 編輯 (1)放縮的方向要一致。(2)放與縮要適度。(3)很多時候只對數列的一部分進行放...
2014年高考的高頻考點——錯位相減法 212數列求和的七種基本方法 218數列通項公式的求法 225用分離常數法解2014年高考題 232用分離常數法求解2014年高考四川卷壓軸...
求和一般有以下5個方法: 1,完全歸納法(即數學歸納法) 2 累乘法 3 錯位相減法 4 倒序求和法 5 裂項相消法遞推數列性質 另外,一個各項均為正數的等比數列...
4.歸納猜想證明法 5.倒序相加法 6.錯位相減法 7.裂項求和法 8.函式法 第七章 解析幾何 1.坐標法 2.曲線定義法 3.待定係數法 4.曲線變換法 5.參數法 6...
數學中的常用方法和思想很多,諸如分離常數法、分離變數法、待定係數法、反客為主法、倒序相加法、錯位相減法、數學歸納法、構造法、對偶法、向量法、類比法、極限...
5.3.2錯位相減法1295.4例題分析1295.4.1等差數列與等比數列1295.4.2列舉法在數列解題中的套用1385.4.3放縮法在數列解題中的套用142...
考點65 裂項相消法求和 考點66 錯位相減法求和 考點67 並項求和法 第六章 不等式 6.1 不等式的性質與解法、基本不等式 考點68 不等式的性質與解法 考點69 ...
易錯點23 用錯位相減法求和時項數處理不當致誤易錯點24 對數列的遞推關係轉換不當致誤易錯點25 數列、不等式綜合題中對不等式的放縮錯誤易錯點26 用錯三角...
我們知道,等比數列前項和公式的推導方法用的是“錯位相減法”.在近幾年的高考中,涉及到錯位相減法的試題有許多,在複習時要特別引起重視.因為加與減互為逆運算,...
11.錯位相減法求Sn 12.裂項(拆項)結合累加(疊加)法,求Sn 13.從函式的角度看Sn,求Sn的最值 有關解法注意點 五、解析幾何 1.結合向量的坐標運算,運...
四、錯位相減法 五、倒序相加法 第6節 遞推數列 一、形如an+1=an+f(n)遞推數列 二、形如an+1== f(n)an遞推數列 三、形如an+1=pa。十q(...
錯位相減法 倒序相加法 裂項求和法 三、數列的遞推關係 四 三角函式 知識網路構建 概念公式定理 一、任意角和弧度制 角的概念 角的分類 象限角 象限界角(終邊...
5.3.2錯位相減法1295.4例題分析1295.4.1等差數列與等比數列1295.4.2列舉法在數列解題中的套用1385.4.3放縮法在數列解題中的套用142...
考點四錯位相減法考點五數列求和的綜合問題考點失分警示熱點題型探究2015熱點預測6.5數列的綜合套用高考精選2015高考考情分析基礎知識整合...
1.定義法 2.換元法 3.消元法 4.待定係數法 5.賦值代換法 (三)數列求和的常用方法 1.降次逐加法 2.展開分組法 3.錯位相減法 4.並項求和...
5.3.2錯位相減法1295.4例題分析1295.4.1等差數列與等比數列1295.4.2列舉法在數列解題中的套用1385.4.3放縮法在數列解題中的套用142...
高中數學學習過程中所接觸到的數學思想方法一般分為三類:第一類是用於解題的具體操作性的方法,如配方法、換元法、消元法、待定係數法、判別式法、錯位相減法、...
