差比數列是由一個等差數列和一個等比數列相乘得到的新數列,其求和是高中數學常考內容。但學生在利用錯位相減法進行差比數列求和時,往往只能寫出前幾步,整理不出最終結果。差比數列求和公式由重慶一中付紅老師推導並解釋結構,可以解決學生利用錯位相減法求差比數列前n項和的計算瓶頸。該公式的另一個優點就是可以無縫融入到學生解題過程中,使解題過程看不出公式痕跡。
基本介紹
- 中文名:差比數列求和公式
- 別稱:錯位相減法求和公式
- 提出者:付紅
- 提出時間:2016年5月9日
- 套用學科:數學
- 適用領域範圍:高中數列求和、錯位相減法
差比數列求和公式的內容:

題目:求數列的前項和。
公式:
結構分析:。此公式看似複雜,實際上結構簡單。僅需對結構配上4個係數即可。而且係數結構也很類似,分別為。
差比數列求和公式的證明:

證明: …………①
則 ………②
,得證。
差比數列求和公式的套用舉例:
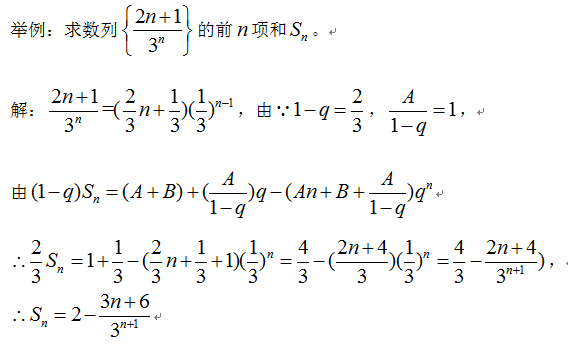
舉例:求數列的前項和。
解:,由,,
由
,
差比數列求和公式的意義:
學生在利用錯位相減法進行差比數列求和時,往往只會前幾步,不能整理出最終結果。此公式書寫方便,可以無縫嵌入到學生的錯位相減求和方法中,以解決學生利用錯位相減法求差比數列前n項和的計算瓶頸。

