基本介紹
- 中文名:重級數
- 外文名:multiple series
- 別稱:多重級數,k重級數
- 所屬學科:高等數學
- 簡介:重序列的形式和
基本介紹
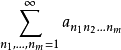
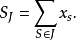
相關性質定理
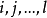
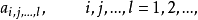




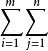






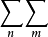


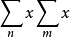
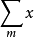
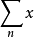

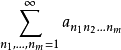
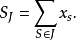
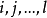
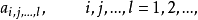




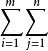






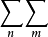


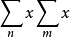
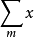
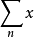
重級數(multiple series)也稱多重級數,k重級數等,是重序列的形式和,多重級數的理論和性質等可效仿二重級數的理論和性質加以推廣得到。...
在數學中,泰勒級數(英語:Taylor series)用無限項連加式——級數來表示一個函式,這些相加的項由函式在某一點的導數求得。泰勒級數是以於1715年發表了泰勒公式的...
地震級數是芮氏地震規模地震強度大小的一種度量,根據地震釋放能量多少來劃分。目前國際上一般採用美國地震學家查爾斯·弗朗西斯·芮希特和賓諾·古騰堡(Beno Gutenberg...
傅立葉級數是一類特殊的三角級數。當n≥2時,常稱σ(f)為多重傅立葉級數。...... 傅立葉級數是一類特殊的三角級數。當n≥2時,常稱σ(f)為多重傅立葉級數...
斐波那契級數編輯 鎖定 歐洲數學在希臘文明衰落之後長期處於停滯狀態,直到12世紀才有復甦的跡象。這種復甦開始是受了翻譯、傳播希臘、阿拉伯著作的刺激。對希臘與東方...
疊級數(repeated series)亦稱累級數,指各項均為級數的級數,即表達式∑∞m=1∑∞n=1amn,其中{amn}為二重序列。對疊級數,可以用普通級數的有關概念來定義其收斂...
正項級數,是一種數學用語。在級數理論中,正項級數是非常重要的一種,對一般級數的研究有時可以通過對正項級數的研究來獲得結果,就像非負函式廣義積分和一般廣義...
內容介紹本教材內容包括級數和拉普拉斯變換,每章前有學習指南,章後有本章小結和數學實驗,便於學生自學,教材內容充實,結構合理,在敘述上既注重知識的體系,又注重理論...
即T=T0+T1+…,級數的零階項$ {T}_{0}=\frac{R}{4\pi }{\int }_{\sigma }\Delta gS\text{(}\psi \text{)}\mathrm{d}\sigma \text{,}$T0=...
注:本詞條翻譯至wikipedia.沃爾泰級數是非線性行為中的一種模型,類似於泰勒級數。它不同於泰勒級數的地方在於能夠捕捉記憶效應。在非線性系統中,泰勒級數能夠用於對...
冪級數概念在多元微積分學中的一個推廣是多元冪級數...... 級數概念在多元微積分學中的一個推廣是多元冪級數 ...在多重下標的表示法中,則有多元冪級數 多元冪...
多重指標是數學中一種方便的表示法,它將指標中的單個整數推廣為多個整數,它可以簡化多元微積分、偏微分方程與分布理論中的計算,也便於操作冪級數。...
多重極點洛朗級數 編輯 在數學中,複變函數 的洛朗級數,是冪級數的一種,它不僅包含了正數次數的項,也包含了負數次數的項。有時無法把函式表示為泰勒級數,但可以...
