重序列(multiple sequence)是二重序列的推廣,即定義在N×N×…×N上的n元函式序列,當n≥2時,稱為(多)重序列。n=1時,即通常的序列也稱為簡單序列,有關多重數列的概念、性質,與二重數列類似。
基本介紹
- 中文名:重序列
- 外文名:multiple sequence
- 所屬學科:數學
- 簡介:二重序列的推廣
- 別稱:多重序列
- 相關概念:序列
基本介紹



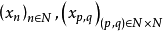
二重序列



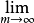


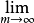



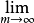


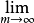

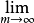

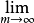

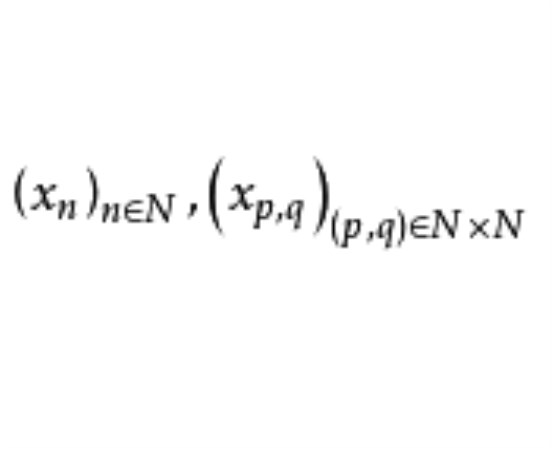
重序列(multiple sequence)是二重序列的推廣,即定義在N×N×…×N上的n元函式序列,當n≥2時,稱為(多)重序列。n=1時,即通常的序列也稱為簡單序列,有關多重數列的概念、性質,與二重數列類似。



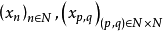



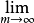


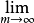



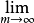


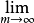

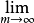

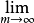

重序列(multiple sequence)是二重序列的推廣,即定義在N×N×…×N上的n元函式序列,當n≥2時,稱為(多)重序列。n=1時,即通常的序列也稱為簡單序列,有關多...
多重序列比對(Multiple sequence alignment;MSA)是對三個以上的生物學序列(biological sequence),如蛋白質序列、DNA序列或RNA序列所作的序列比對。一般來說,是輸入一...
《生物序列突變與比對的結構分析》共分三部分介紹,第一部分介紹序列圖便於比對的結構模型;第二部分介紹序列的比對算法與結構分析;第三部分是有關隨機分析與圖論的...
《第一序列》是閱文集團大神作家會說話的肘子繼《大王饒命》後的最新作品。這次是一個新的故事。浩劫餘生,終見光明。講述了一個“主角任小粟通過吸收正能量一步步...
為確定兩個或多個序列之間的相似性以至於同源性,而將它們按照一定的規律排列。將兩個或多個序列排列在一起,標明其相似之處。序列中可以插入間隔(通常用短橫線“-...
德布萊英序列(de Bruijn sequence)亦稱完全循環,是一類特殊的組合序列,一個循環是一個依圓周順序的序列a₁a₂…ar,即a1在ar之後,且a2…ara1,…,ara1…ar-...
φ收斂序列(φ-convergent sequence)是關於絕對值φ的收斂序列。收斂序列是有有限極限的序列。稱{an}是收斂序列,只說明它有有限極限,並未說明其極限值是什麼。序列...
侵華日軍戰鬥序列,步兵小隊轄一個機槍組(二挺輕機槍)、一個擲彈筒組(二個擲彈筒)和二個步槍組。每挺輕機槍編制四人(指揮官、射手、兩名攜彈藥的副射手),每具...
“職務序列”即職務的層次和職務的級別,一般包括共有職務序列(領導職務)和專有職務序列(綜合管理類非領導職務、行政執法職務、專業技術職務)兩大類。也就是說,...
序列相關性,在計量經濟學中指對於不同的樣本值,隨機干擾之間不再是完全相互獨立的,而是存在某種相關性。又稱自相關(autocorrelation),是指總體回歸模型的隨機誤差項...
定義介紹 序列集合記號(notation of sequence sets)以正整數為分量的有限序列集合的記號.下面是多重線性代數中常用的序列集合及記號: 上面這些集合的序列數目分別為:...
脈衝控制序列是一種離散的非線性開關變換器控制方法,具有瞬態回響快、無需補償網路、控制電路實現簡單等優點.。根據控制脈衝的產生方式不同,脈衝控制序列可分為電壓...
遺傳學上講的回文序列指的是雙鏈DNA或RNA分子中的特定的核苷酸片段,該片段在其中一條鏈上按5'到3'讀取的序列與其互補鏈上按相同的5'到3'讀取的序列一致。回文...
反向重複序列指兩個序列相同的拷貝在DNA鏈上呈反向排列, 是DNA重複序列的一種類型。反向重複序列散布在整個基因組中,約占人類基因組中占5%,常見於基因的調控區,...
空間序列是指空間的先後順序,是設計師按建築功能給予合理組織的空間組合。各個空間之間有著順序、流線和方向的聯繫。空間序列設計的構思、布局以至處理手法是根據空間...
如果一個序列,一方面它是可以預先確定的,並且是可以重複地生產和複製的;一方面它又具有某種隨機序列的隨機特性(即統計特性),我們便稱這種序列為偽隨機序列。...
把兩個以上字元序列對齊,逐列比較其字元的異同,使得每一列的字元儘可能一致,以發現其共同的結構特徵的方法稱為多序列比對。多序列比對問題是雙序列比對問題的推廣...
《刀劍神域 -序列之爭-》是由A-1 Pictures製作的動畫電影,由伊藤智彥執導。伊藤智彥與《刀劍神域》輕小說原作者川原礫共同譜寫了劇本,劇情為原創,講述了原作...
序列化 (Serialization)是將對象的狀態信息轉換為可以存儲或傳輸的形式的過程。在序列化期間,對象將其當前狀態寫入到臨時或持久性存儲區。以後,可以通過從存儲區中...
重級數(multiple series)也稱多重級數,k重級數等,是重序列的形式和,多重級數的理論和性質等可效仿二重級數的理論和性質加以推廣得到。...
φ稱為二重序列{amn}到序列 的重排,或二重級數(1)到單級數∑aφ(k)的重排。若級數|amn|, |amn|, |amn|, |aφ(k)|之一收斂,則:...
CLUSTALX-是CLUSTAL多重序列比對程式的Windows版本。...... CLUSTALX-是CLUSTAL多重序列比對程式的Windows版本。中文名 Clustalx 套用 是構建系統發育樹的前提 主要功...
重組質粒的構建及序列分析關鍵字:單純皰疹病毒 胸苷激酶基因 缺失突變序列分析摘要:目的:構建HSV-1型胸苷激酶基因部分缺失的重組質粒並進行序列測定。 方法:以pUC18/...
在套用鬆弛疊代法重構序列的情況中,有時,該序列雖然滿足唯一恢復的條件,但是,疊代並不收斂。在分析不收斂的原因時發現,在單位圓上的零點有著特殊的性質,它使在該...
全基因組重測序是對已知基因組序列的物種進行不同個體的基因組測序,並在此基礎上對個體或群體進行差異性分析。SBC將不同梯度插入片段(Insert-Size)的測序文庫結合...
