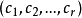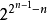德布萊英序列(de Bruijn sequence)亦稱完全循環，是一類特殊的組合序列，一個循環是一個依圓周順序的序列a1a2…ar，即a1在ar之後，且a2…ara1，…，ara1…ar-1都是與a1a2…ar相同的循環。
基本介紹
- 中文名：德布萊英序列
- 外文名：de Bruijn sequence
- 所屬學科：數學（組合學）
- 別稱：完全循環
- 簡介：一類特殊的組合序列
基本介紹,De Bruijn序列的套用與性質簡介,德布萊英定理,德布萊英圖,
基本介紹
設n是正整數，N=2n，一個由數碼0和1組成的循環a1a2…aN，即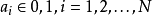
，若子序列
就是所有可能的N個由數碼0和1組成的有序序列b1b2…bn，則稱該循環是一個完全循環或德布萊英序列，例如n=1時，循環01;n=2時，循環0011，n=3時，循環00010111和00011101均為德布萊英序列。關於德布萊英序列的主要問題是：對任意正整數n，長為N=2n的德布萊英序列是否存在?若存在，有多少個?德布萊英定理斷言：對每個正整數n，恰存在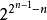
次冪個長為N=2n的完全循環。事實上，每個長為N=2n的德布萊英序列恰與德布萊英圖Gn中的一條完全迴路相對應。
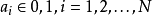
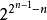
De Bruijn序列的套用與性質簡介
De Bruijn序列是一類重要的非線性移位暫存器序列，它在通信及密碼等領域內有著極為廣泛的套用，複雜度是刻劃這類序列特性的一個重要概念。具有良好偽隨機性質的二元序列廣泛套用於通信、密碼學等多個領域中，例如在流密碼中我們就需要好的二元序列來做為密鑰流。分析和構造具有良好性質的二元序列一直是序列研究中的重要問題。
二元de Bruijn序列是一種特殊的周期為2n的序列，滿足任意一個二元n長向量都在de Brujn序列的一個周期中恰出現一次。 De Bruijn序列具有許多很好的偽隨機性質，在圖論、DNA存儲技術、通信與密碼學中都有重要套用。De Bruijn序列雖然看起來非常簡單，但對它的深入分析卻是非常困難的，尋找de Bruijn序列的新的刻畫和性質，以及尋找新的能更有效地生成更多的de Bruijn序列的算法一直是 de Bruijn序列的研究重點。
一個二元n階de Bruijn序列s是一個周期為2n的序列，滿足任意一個二元n長向量或n元組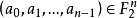
，都在S的一個周期中出現恰好一次。
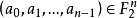
De Bruijn序列具有許多良好的性質：
1)大周期，2n，它是n階FSR能夠生成的序列的最大周期；
2)平衡性，0和1都出現2n-1次；
3)n元組平衡性，每個二元n長向量都出現一次；
4)大線性複雜度，它的線性複雜度c(s)滿足2n-1+n≤c(s)≤2n-1；
5)De Brujn序列的個數非常多，總個數為。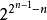
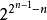
因此，de Bruijn序列在圖論、DNA排序存儲技術、通信與密碼學等多個領域中都有重要套用。
德布萊英定理
德布萊英定理是波利亞定理的推廣，若兩置換群A和B分別作用於兩有限集X={x1，x2，…，xn}和Y={y1，y2，…ym}，則可定義冪群BA={(α，β)|α∈A，β∈B}對函式集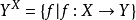
的作用為
。若有
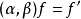，則稱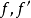
是等價的，記為
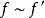，~為一等價關係。於是，YX被分為若干等價類之並，這些等價類稱為函式式樣或函式軌道，德布萊英定理斷言：函式式樣的個數等於
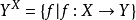
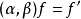
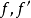
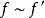
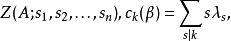
其中β的型為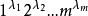
。
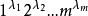
哈拉里(F.Harary)推廣了德布萊英定理。
設Y為可數集，Y至少含2元，定義權函式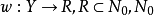
為非負整數集；又定義函式f的權
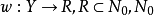
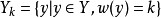
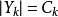
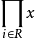
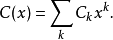
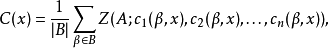
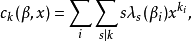
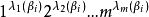
德布萊英圖
德布萊英圖是一種重要的圖，是由(0，1)序列衍生的圖.由數碼0和1組成的序列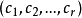
稱為一個(0，1)序列，r稱為該序列的長.長為n-1的(0，1)序列總計2n-1個.設每個這樣的(0，1)序列(c1，c2，…，cn-1)與一個頂點pi相對應，這裡1≤i≤2n-1.設每個長為n的(0，1)序列(b1，b2，…，bn-1，bn)與一個起點為(b1，b2，…，bn-1)、終點為(b2，b3，…，bn)的有向弧相對應.稱具有頂點集{pi：i=1，2，…，2n-1}和上述對應有向弧集的有向圖為一個德布萊英圖，記為Gn.圖示為G3.Gn為有向連通圖，且每個頂點處恰有兩條入弧和兩條出弧.通過給定有向圖中每一有向弧恰一次的迴路，稱為該圖的一條有向完全迴路.Gn中的有向完全迴路與長為N=2n的德布萊英序列一一對應，德布萊英(N.G.de Bruijn)證明：Gn恰有
