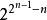德布萊英圖

德布萊英圖(de Bruijn graph)是一種重要的圖，是由(0，1)序列衍生的圖。由數碼0和1組成的序列(c₁，c₂，…，c_r)稱為一個(0，1)序列，r稱為該序列的長，長為n-1的(0，1)序列總計2^n-1個，設每個這樣的(0，1)序列(c₁，c₂，…，c_n-1)與一個頂點p_i相對應，這裡1≤i≤2^n-1。設每個長為n的(0，1)序列(b₁，b₂，…，b_n-1，b_n)與一個起點為(b₁，b₂，…，b_n-1)、終點為(b₂，b₃，…，b_n)的有向弧相對應，稱具有頂點集{p_i：i=1，2，…，2^n-1}和上述對應有向弧集的有向圖為一個德布萊英圖，記為G_n。G_n為有向連通圖，且每個頂點處恰有兩條入弧和兩條出弧，通過給定有向圖中每一有向弧恰一次的迴路，稱為該圖的一條有向完全迴路，G_n中的有向完全迴路與長為N=2ⁿ的德布萊英序列一一對應，德布萊英(N.G.de Bruijn)證明：G_n恰有2的2^n-1-n次方條有向完全迴路。

基本介紹

• 中文名：德布萊英圖
• 外文名：de Bruijn graph
• 別名：de Bruijn圖
• 所屬學科：數學(組合學)
• 簡介：由(0，1)序列衍生的圖

德布萊英圖的概念

定義n維d進位有向de Bruijn圖是標號圖，記作B(d，n）(d≥2，n≥1)，其結點集記作V_B(d,n)，邊集記作E_B (d,n)，且

，且

如圖1所示：

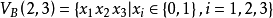
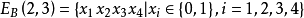
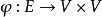
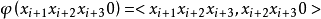
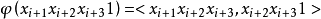
圖1

例1 n維2進位有向de Bruijn圖B（2，n），其中

，且

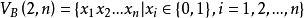
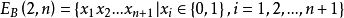
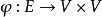
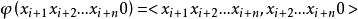
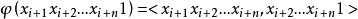
德布萊英圖的鄰接矩陣

下面來考察有向de Bruijn圖B（2，n）的鄰接矩陣。顯然，n維2進位有向de Bruijn圖B(2，n)是有2ⁿ個結點的有向圖，且這2ⁿ個結點恰是2ⁿ個長度為n的二進制數，其中每個結點的入度和出度均為2。若將這2ⁿ個結點依次對應為0，1，2，…．2ⁿ-1，於是，從結點0到結點0與1各有一條有向邊，從結點1到結點2與3各有一條有向邊，…，從結點2^n-1-1到結點2ⁿ-2與2ⁿ-1各有一條有向邊；而從結點2^n-1到結點0與1各有一條有向邊，從結點2^n-1+1到結點2與3各有一條有向邊，…，從結點2ⁿ-1到結點2ⁿ-2與2ⁿ-1各有一條有向邊。因此有向de Bruijn圖B(2，n)的鄰接矩陣為

另一方面，有向de Bruijn圖B(2，”)的結點和邊的關係如圖3.3.2所示。任取有向de Bruijn圖B(2，，？)的兩個結點T與y，顯然1’與y總是長為n的二進制數0---000.0---001.0---010，…，1-- - 110，1...111中的某一個，於是從圖3.3.2知，從任意結點J‘到任意結點y有且僅有一條長度為n的有向鏈，因而由定理2.5.1得到如下定理。

定理1 設n維2進位有向de Bruijn圖B（2，n）（d≥2，n≥1）的鄰接矩陣為A，則矩陣Aⁿ的任意i行j列元素均為1，其中i，j=1，2，…，2ⁿ。

一般地，n維d進位有向de Bruijn圖B(d，n)是有dⁿ個結點的有向圖，且每個結點的入度和出度均為d。

定理2 設n維d進位有向dc Bruijn圖B（d，n）（d≥2，n≥1）的鄰接矩陣為A，則矩陣Aⁿ的任意i行j列元素均為1，其中i，j=1，2，…，dⁿ。

de Bruijn圖的譜

求一般圖的譜問題是非常困難的，即使對一些特殊圖類的譜計算也很不容易。de Bruijn圖在計算機磁鼓設計、編碼、VLSI結構設計等領域有著廣泛的套用，同時，de Bruijn圖與超立方體，被認為是真正大型下一代多計算機系統的網際網路。然而，de Bruijn圖的內涵非常豐富，它的許多參數還不十分清楚，下面介紹有向dcBruijn圖B(d，n)(d≥2，n≥1)的譜，該結論是由殷劍宏得出的。

定義 設A是任意n階圖G的鄰接矩陣，矩陣A的特徵多項式稱為圖G的特徵多項式；A的特徵值稱為圖G的特徵值；A的譜稱為圖G的譜。

定理3 設D是有向圖，且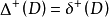，則:

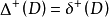
(1)k是D的一個特徵值；

(2)對於D的任意特徵值λ，均有|λ|≤k。

定理4 設λ是實方陣A的特徵值，則λ^k是A^k的特徵值。

定理5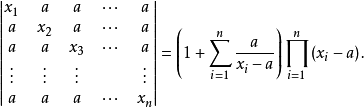

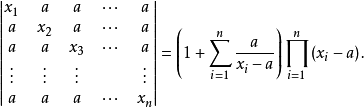
定理6 設n維d進位有向de Bruijn圖B（d，n）（d≥2，n≥1）的鄰接矩陣為A，則矩陣Aⁿ的譜為

其中dⁿ-1與1分別為特徵值0與dⁿ的重數。

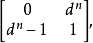
定理7 n維d進位有向de Bruijn圖B（d，n）（d≥2，n≥1）的譜為

其中dⁿ-1與1分別為特徵值0與d的重數。

德布萊英序列

德布萊英序列(de Bruijn sequence)亦稱完全循環，是一類特殊的組合序列，一個循環是一個依圓周順序的序列a₁a₂…a_r，即a₁在a_r之後，且a₂…a_ra₁，…，a_ra₁…a_r-1都是與a₁a₂…a_r相同的循環.設n是正整數，N=2ⁿ，一個由數碼0和1組成的循環a₁a₂…a_N，即a_i∈{0，1}，i=1，2，…，N，若子序列a_ia_i+1…a_i+n-1(i=1，2，…，N)就是所有可能的N個由數碼0和1組成的有序序列b₁b₂…b_n，則稱該循環是一個完全循環或德布萊英序列。例如n=1時，循環01；n=2時，循環0011，n=3時，循環00010111和00011101均為德布萊英序列。

關於德布萊英序列的主要問題是：對任意正整數n，長為N=2ⁿ的德布萊英序列是否存在?若存在，有多少個?德布萊英定理斷言：對每個正整數n，恰存在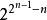 個長為N=2的完全循環，事實上，每個長為N=2ⁿ的德布萊英序列恰與德布萊英圖G_n中的一條完全迴路相對應(見上文“德布萊英圖”)。