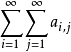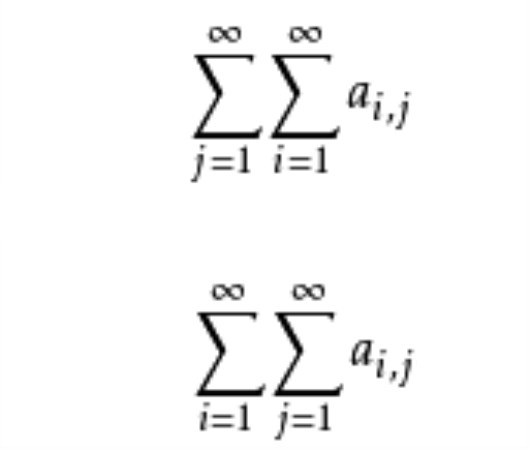疊級數

疊級數(repeated series)亦稱累級數，指各項均為級數的級數，即表達式∑^∞_m=1∑^∞_n=1a_mn，其中{a_mn}為二重序列。對疊級數，可以用普通級數的有關概念來定義其收斂性及其他概念。例如，對於∑^∞_m=1∑^∞_n=1a_mn，若對每個m，級數∑a_mn收斂於b_m，且級數∑b_m收斂，則稱∑^∞_m=1∑^∞_n=1a_mn收斂，其和為∑b_m的和。若∑^∞_m=1∑^∞_n=1|a_mn|收斂，則稱∑^∞_m=1∑^∞_n=1a_mn絕對收斂。從一個疊級數收斂不能得到由同一個二重序列導出的另一疊級數收斂，即使都收斂也不一定彼此相等。例如，按如下定義a_mn：n=m+1時，a_mn=1，m=n+1時，a_mn=-1，對其他m與n，a_mn=0，則相應兩個疊級數分別收斂於1與-1.當a_mn≥0(m，n∈N)時，∑_m∑_na_mn=∑^∞_ka_φ(k)(可以是+∞)，其中φ是N到N×N上的任意一一對應，又，若二重級數∑^∞_m=1∑^∞_n=1a_mn收斂，對每個m，級數∑a_mn也都收斂，則∑^∞_m=1∑^∞_n=1a_mn收斂，且∑^∞_m,n=1a_mn=∑_m∑_na_mn。

基本介紹

• 中文名：疊級數
• 外文名：repeated  series
• 別稱：累級數
• 所屬學科：數學
• 簡介：各項均為級數的級數
• 所屬問題：數學分析（無窮級數）

基本介紹

若將無窮矩陣中的某一行元素依次相加，所得級數

稱為行級數(repeated series by rows)。再將行級數依次相加，所得運算符號：

稱為疊級數(repeated series)或累級數。自然，交換次序可得另一種疊級數

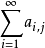
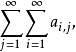
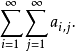
疊級數的收斂

①若行級數收斂(設和為A_j)，且級數也收斂(設和為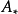)，則稱疊級數收斂，收斂和為。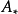

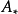
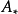
②同樣，若級數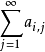收斂(設和為A_i)，且級數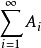也收斂(設和為A*)，則稱疊級數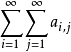收斂，收斂和為A*。

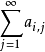
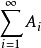
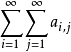
二重級數與累級數的關係

定理1 若二重級數及行級數都收斂，則疊級數也必定收斂，且與二重級數有相同的和數，即

類似地，若二重級數及列級數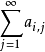都收斂，則疊級數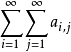也必定收斂，且與二重級數有相同的和數，即

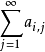
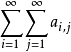
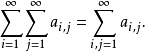
當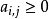時，二重級數稱為正項二重級數，對於正項二重級數的收斂性有下列定理。

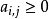
定理2正項級數收斂的充要條件是部分和有上界，即有常數M，使

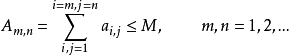
定理3 正項級數與累級數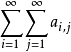，有相同的收斂性及收斂和。