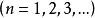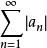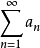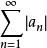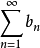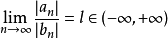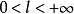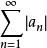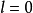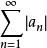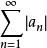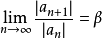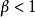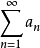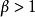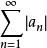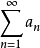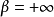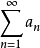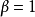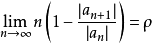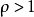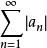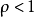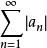若某一任意數項級數的各項的絕對值所組成的級數收斂,則稱該級數為絕對收斂級數。絕對收斂級數是收斂的,但收斂的級數不一定是絕對收斂級數。絕對收斂級數任意交換各項的順序後所構成的新的級數仍舊絕對收斂。通過比較判別法、比值判別法、Raabe判別法等可以判別某一數項級數是否絕對收斂。
基本介紹
- 中文名:絕對收斂級數
- 外文名:Absolutely Convergent Series
- 本質:級數各項的絕對值組成的級數收斂
- 性質1:絕對收斂的級數是收斂的
- 性質2:交換各項順序後所得級數絕對收斂
- 判別法:比較、比值、Raabe判別法等
定義
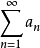
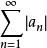
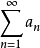
性質
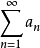
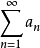
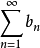

判別法