沃爾泰拉級數

註：本詞條翻譯至wikipedia.

沃爾泰級數是非線性行為中的一種模型，類似於泰勒級數。它不同於泰勒級數的地方在於能夠捕捉記憶效應。在非線性系統中，泰勒級數能夠用於對輸入的回響的逼近，如果在特定的某個時間內，輸出是嚴格取決於輸入的。對於沃爾泰級數，非線性系統的輸出取決於任何其他的時間內的輸入。這種屬性使得其有能力捕捉一些器件的記憶效應，比如電容和電感。

沃爾泰級數被廣泛套用於藥物醫學和生物學，尤其是神經科學。它也被套用於電氣工程學科中內部調製失真的建模。

在數學上，沃爾泰級數表示功能動態的拓展、非線性、時不變泛函。它被頻繁的套用在系統識別。沃爾泰級數，即為無窮個多維卷積的和。

基本介紹

• 中文名：沃爾泰級數
• 外文名：Volterra series

沃爾泰技術可以通過兩種不同的視角來理解：其中一種考慮兩個實函式之間的映射操作，另一種考慮實函式往實數上的映射操作。由於假設的時不變系統，所以後者更為常用。

連續時間

一個連續的時不變系統，輸入x(t)，輸出y(t)即為沃爾泰級數展開：

這裡，通常通過調節合適的輸出量級，常數h_o可以調節為0。函式hn稱為第n階沃爾泰核，其可以當成是該系統高階的脈衝回響函式。如果N是有限的，那么該級數是截斷的。如果a,b,N都是有限的，級數被稱為雙重有限。

離散時間

類似於連續時間：

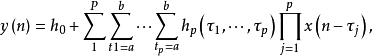
這裡，h_p被稱為離散時間的沃爾泰核，如果P是有限的，級數操作就是截斷的。如果a,b,P都是有限的，那么級操作被稱為雙重有限。