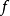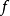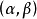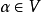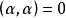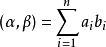酉空間(unitary linear space)是一種特殊的複線性空間。指以一類埃爾米特函式作內積的複線性空間。設V是複數域C上的線性空間，J是C的(共軛)自同構：(a+bi)J=a-bi。若在V上定義了一個關於J的埃爾米特函式，並且對任意α∈V，內積(α，α)≥0及(α，α)=0 若且唯若α=0，則稱V為酉空間。n維酉空間U中總存在標準正交基。對U的任一線性變換σ，都存在它的共軛變換σ*。若以A，B分別表示σ與σ*關於給定基的矩陣，則A=G′-1B-′G′，這裡G是關於給定基的格拉姆矩陣，B-′是B的轉置共軛矩陣。對U的任一正規(埃爾米特)變換σ，都存在標準正交基，使σ關於此基的矩陣為對角形(實對角形)矩陣。
基本介紹
- 中文名：酉空間
- 外文名：unitary linear space
- 領域：數學
- 本質：複線性空間
- 對象：埃米爾特函式
- 矩陣：格拉姆矩陣
線性空間,詳細定義,函式定義,函式性質,
線性空間
亦稱向量空間。它是線性代數的中心內容和基本概念之一。設V是一個非空集合，P是一個域。若：
1.在V中定義了一種運算，稱為加法，即對V中任意兩個元素α與β都按某一法則對應於V內惟一確定的一個元素α+β，稱為α與β的和。
2.在P與V的元素間定義了一種運算，稱為純量乘法(亦稱數量乘法)，即對V中任意元素α和P中任意元素k，都按某一法則對應V內惟一確定的一個元素kα，稱為k與α的積。
3.加法與純量乘法滿足以下條件：
1) α+β=β+α，對任意α，β∈V.
2) α+(β+γ)=(α+β)+γ，對任意α，β，γ∈V.
3) 存在一個元素0∈V，對一切α∈V有α+0=α，元素0稱為V的零元.
4) 對任一α∈V，都存在β∈V使α+β=0，β稱為α的負元素，記為-α.
5) 對P中單位元1，有1α=α(α∈V).
6) 對任意k，l∈P，α∈V有(kl)α=k(lα).
7) 對任意k，l∈P，α∈V有(k+l)α=kα+lα.
8) 對任意k∈P，α，β∈V有k(α+β)=kα+kβ，
則稱V為域P上的一個線性空間，或向量空間。V中元素稱為向量，V的零元稱為零向量，P稱為線性空間的基域.當P是實數域時，V稱為實線性空間。當P是複數域時，V稱為複線性空間.例如，若V為三維幾何空間中全體向量(有向線段)構成的集合，P為實數域R，則V關於向量加法(即平行四邊形法則)和數與向量的乘法構成實數域R上的線性空間。又如，若V為數域P上全體m×n矩陣組成的集合Mmn(P)，V的加法與純量乘法分別為矩陣的加法和數與矩陣的乘法，則Mmn(P)是數域P上的線性空間.V中向量就是m×n矩陣。再如，域P上所有n元向量(a1，a2，…，an)構成的集合P對於加法：(a1，a2，…，an)+(b1，b2，…，bn)=(a1+b1，a2+b2，…，an+bn)與純量乘法：λ(a1，a2，…，an)=(λa1，λa2，…，λan)構成域P上的線性空間，稱為域P上n元向量空間。
線性空間是在考察了大量的數學對象(如幾何學與物理學中的向量，代數學中的n元向量、矩陣、多項式，分析學中的函式等)的本質屬性後抽象出來的數學概念，近代數學中不少的研究對象，如賦范線性空間、模等都與線性空間有著密切的關係。它的理論與方法已經滲透到自然科學、工程技術的許多領域。哈密頓(Hamilton，W.R.)首先引進向量一詞，並開創了向量理論和向量計算。格拉斯曼(Grassmann，H.G.)最早提出多維歐幾里得空間的系統理論。1844—1847年，他與柯西(Cauchy，A.-L.)分別提出了脫離一切空間直觀的、成為一個純粹數學概念的、抽象的n維空間。特普利茨(Toeplitz，O.)將線性代數的主要定理推廣到任意域上的一般的線性空間中。
詳細定義
酉空間(unitary linear space)是一種帶有正定埃爾米特型的複線性空間V。設V是複數域C上的線性空間。為使得V成為類似於歐幾里得空間的度量空間，也就是希望複數域上非零向量的度量是正實數，我們需要引入埃爾米特函式(也稱埃爾米特型)。
若複線性空間V上的埃爾米特型
滿足：
把酉空間中取定的正定埃爾米特型稱為內積，記為
。對任意
，內積
，若且唯若
。
酉空間(unitary linear space)是一種特殊的複線性空間。指以一類埃爾米特函式作內積的複線性空間。設V是複數域C上的線性空間，J是C的(共軛)自同構：(a+bi)J=a-bi。若在V上定義了一個關於J的埃爾米特函式，並且對任意α∈V，內積(α，α)≥0及(α，α)=0 若且唯若α=0，則稱V為酉空間。n維酉空間U中總存在標準正交基。對U的任一線性變換σ，都存在它的共軛變換σ*。若以A，B分別表示σ與σ*關於給定基的矩陣，則A=G′-1B-′G′，這裡G是關於給定基的格拉姆矩陣，B-′是B的轉置共軛矩陣。對U的任一正規(埃爾米特)變換σ，都存在標準正交基，使σ關於此基的矩陣為對角形(實對角形)矩陣。
設V是複數域C上的線性空間.若對於V中任意兩個向量α，β，都有惟一確定的複數，記為(α，β)，與它們對應，且滿足：
2.(kα，β)=k(α，β)；
3.(α+β，γ)=(α，γ)+(β，γ)；
4.(α，α)是非負的實數，且(α，α)=0，若且唯若α=0，其中α，β，γ是V中的任意向量，k為任意複數；則稱(α，β)是α與β的內積。定義了內積的複線性空間V稱為酉空間。例如，在復n維向量空間C中，對任意α=(a1，a2，…，an)，β=(b1，b2，…，bn)，定義：
則(α，β)是C上的內積，而C是酉空間。在n維酉空間中，可以定義正交基和標準正交基。n(>0)維酉空間的標準正交基是存在的。
函式定義
埃爾米特函式是一種特殊的半雙線性函式。設V是域P上的線性空間，J是P的自同構，φ是V上的半雙線性函式，若J=J^-1且對每對α1，α2∈V，φ(α1，α2)=φ(α2，α1)，則稱φ為V上的埃爾米特函式；當J=J^-1且φ(α1，α2)=-φ(α2，α1)時，稱φ為反埃爾米特函式。特別地，當J為恆等自同構時，埃爾米特(反埃爾米特)函式就是對稱(反對稱)雙線性函式。n維線性空間V上的埃爾米特(反埃爾米特)函式對取定基的矩陣是埃爾米特(反埃爾米特)矩陣。
函式性質
用V表示酉空間，T*表示T的共軛變換。
定義1 T是V的線性變換，如果對V中任意向量α,β，有(Tα,Tβ)=(T*α,T*β)成立,則稱T是V的正規變換。
定理1 設T是V的線性變換，則下列命題等價：
(Ⅰ) T是正規變換；(Ⅱ) T* T= TT*；(Ⅲ) T在標準正交基下的矩陣是正規矩陣。
證明 先證(Ⅰ)→ (Ⅱ)
“ →”：設對V中任意的向量α,β，因(Tα,Tβ)=(T*α,T*β)，於是(α,T T*β)=(T*α,T*β)=(Tα,Tβ)=(α,T*Tβ)，即(α,TT*β- T*Tβ)= 0。
由α的任意性得TT*β- T*Tβ= 0，即TT*β= T* Tβ，又由β的任意性得TT* = T* T；
“← ”：對V中任意的向量α,β，因T* T= TT*,故有(Tα,Tβ)=(α,T*Tβ)=(α,TT*β)=(T*α,T*β)，所以T是正規變換。
再證(Ⅱ) →(Ⅲ)
設T在標準正交基ε1,ε2,… ,εn下的矩陣為A，則T*在ε1,ε2,… ,εn下的矩陣為A′，即：
T(ε1,ε2,… ,εn)=(ε1,ε2,… ,εn)A (1)
T*(ε1,ε2,…εn)=(ε1,ε2,… ,εn)A′ (2)
即有：
T* T(ε1,ε2,… ,εn)= T*(ε1,ε2,… ,εn)A=(ε1,ε2,… ,εn)A′A (3)
TT*(ε1,ε2,… ,εn)= T(ε1,ε2,… ,εn)A′=(ε1,ε2,… ,εn)AA′ (4)
由(3)、(4)可知，當TT* = T*T時，有A′A= AA′，即A是正規矩陣。當A′A= AA′時，顯然也有TT*= T*T，即T是正規變換。
定理2 設T是正規變換，λ為複數，設I是單位變換，則：(Ⅰ)λT是正規變換；(Ⅱ) T-λI也是正規變換。
證明 (Ⅰ)因(λT)* = λT*,所以(λT)(λT)* = λT λT* = λ· λ(T·T*)= λ λ(T*T)=( λT*)(λT)=(λT)*(λT)。即λT是正規變換。
(Ⅱ)因(T- λI)(T- λI)* =(T-λI)(T*- λI)= TT*-λIT*- T( λI)+λI· λI= TT*-λT*-λT+ λ λI= T*T- λT*- λT+ λ λI= T*(T- λI)- λ(T- λI)=(T*- λI)(T- λI)=(T- λI)*(T- λI)，即T- λI也是正規變換。
定理3 設T1,T2是正規變換，當T*1與T2可交換時，T1+ T2是正規變換，T1T2也是正規變換。
證明 當T*1T2= T2T*1時，有T1T*2=(T2T*1)* =(T1*T2)* = T2*T1，故：
(T1+ T2)(T1+ T2)* =(T1+ T2)(T*1+ T*2)= T1(T*1+ T*2)+ T2(T*1+ T*2)= T1T*1+ T1T*2+T2T*1+ T2T*2= T*1T1+ T*2T1+ T*1T2+ T*2T2=(T*1+ T*2)T1+(T*1+ T*2)T2=(T*1+ T*2)(T1+T2)=(T1+ T2)*(T1+ T2)，所以，T1+ T2也是正規變換。
又(T1T2)(T1T2)* = T1T2T*2T*1= T1T*2T2T*1= T*2T1T*1T2= T*2T*1T1T2=(T1T2)*(T1T2)，所以，T1T2也是正規變換。
