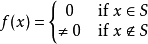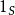遞歸集合

在C語言中，位段的聲明和結構（struct）類似，但它的成員是一個或多個位的欄位，這些不同長度的欄位實際儲存在一個或多個整型變數中。在聲明時，位段成員必須是整形或枚舉類型（通常是無符號類型），且在成員名的後面是一個冒號和一個整數，整數規定了成員所占用的位數。位域不能是靜態類型。不能使用&對位域做取地址運算，因此不存在位域的指針，編譯器通常不支持位域的引用（reference）。

基本介紹

• 中文名：遞歸集合
• 領域：計算機

定義

自然數的子集S被稱為遞歸的，如果存在一個全可計算函式

使得

換句話說，集合S是遞歸的，若且唯若指示函式 是可計算的。

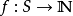
例子

• 空集
  
• 自然數
  
• 自然數的所有有限子集（有限子集並非可數子集，後者可能有無限多的元素）
  
• 素數的集合
  
• 遞歸語言是在形式語言字母表之上所有可能詞的集合中的遞歸集合。
  

性質

如果A是遞歸集合，則A的補集是遞歸集合。 如果A和B是遞歸集合，則A∩B、A∪B和A×B是遞歸集合。集合A是遞歸集合，若且唯若A和A的補集是遞歸可枚舉集合。一個遞歸集合在全可計算函式下的原像（preimage）是遞歸集合。

遞歸函式

一種計算過程，如果其中每一步都要用到前一步或前幾步的結果，稱為遞歸的。用遞歸過程定義的函式，稱為遞歸函式，例如連加、連乘及階乘等。凡是遞歸的函式，都是可計算的，即能行的。

古典遞歸函式，是一種定義在自然數集合上的函式，它的未知值往往要通過有限次運算回歸到已知值來求出，故稱為“遞歸”。它是古典遞歸函式論的研究對象

遞歸可枚舉集合

遞歸可枚舉集，又稱部分遞歸集。在能行性理論中，基本概念是遞歸函式，它可刻畫為：任給x，只要它在x處有定義必可在有限步驟內求出其值。因此遞歸全函式（即處處有定義的）必可在有限步驟內求出它的任一值，至於遞歸部分函式（未必處處有定義的）則只要求有定義處可求出其值，但不要求能夠在有限步驟內判定它的定義域的元素，即對任給的x判定x是否屬於函式的定義域。