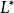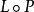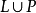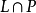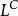遞歸語言

在數學、邏輯和計算機科學中，遞歸語言或遞迴語言是也叫做可判定語言或圖靈可判定語言的形式語言類型。所有遞歸語言的類經常被稱為 R。這種語言類型在喬姆斯基層級中沒有定義。

基本介紹

• 中文名：遞歸語言
• 又稱：圖靈可判定語言
• 性質：形式語言類型
• 領域：計算機

定義

遞歸語言有兩種等價的主要定義：

遞歸語言是在形式語言的字母表上的所有可能的字的集合的遞歸子集。

設S⊆ Σ是一個語言，M是一台圖靈機， 若對於任何字元串 ω ∈ Σ，有

1. ω ∈S若且唯若M接受 ω
   
2. ω ∉S若且唯若M拒絕 ω
   

則稱M判定語言S。 若存在這樣的M，S就稱為圖靈可判定語言。

閉包性質

遞歸語言是在下列運算下是閉合的。就是說，如果L和P是兩個遞歸語言，則下列語言也是遞歸的：

L的Kleene星號：

L的非刪除(non-erasing)同態：φ(L)

L和P的串接：

並集：

交集：

L的補集：

差集：

圖靈可判定語言與圖靈可識別語言的關係

注意圖靈可判定語言和圖靈可識別語言的區別：若S是圖靈可識別語言，則只需存在一 台圖靈機M，當M的輸入 ω ∈S時，M一定會 停機並進入接受狀態；當M的輸入 ω ∉S時，M可能停 機並進入拒絕狀態，或者永不停機。而若S是圖靈可判定語言，則必須存在圖靈機M， 使得對於任意輸入串 ω ∈ Σ，M總能停機，並根據 ω 屬於或不屬於S分別進入接受或拒絕狀態。

定理：存在圖靈不可判定語言。

證明：定義語言 HALTING 如下：

• HALTING = { <M,x> |M是一台圖靈機，x是一個字元串，且M在輸入x上可以停機}
  

其中 <M,x> 表示將M的編碼和串x以某種方式配對而得到的串。 可以證明 HALTING 是圖靈不可判定語言。

下列定理表明了圖靈可判定語言和圖靈可識別語言的關係。

定理：一個語言是圖靈可判定的若且唯若它和它的補語言都是圖靈可識別的。

證明：若S是圖靈可判定的，顯然S和S的補都是圖靈可識別的。 下面假設存在圖靈機M₁和M₂分別識別S和S的補，我們可以構造一個圖靈機M如下：

M= 對於輸入 ω

1. 對於i= 1, 2, 3, ... 分別重複以下步驟：
   
2. 將 ω 作為M₁的輸入，模擬運行M₁，如果M₁可以在i步之內接受 ω，則M進入接受狀態並停機；
   
3. 將 ω 作為M₂的輸入，模擬運行M₂，如果M₂可以在i步之內接受 ω，則M進入拒絕狀態並停機。
   

很顯然，對於任何 ω，它要么屬於S，要么屬於S的補， 所以M₁和M₂中必然有且僅有一個 可以在有限步執行內接受 ω 。 若M₁在k步內接受 ω，說明 ω 屬於S， 則當i=k時，M會接受 ω 並停機； 同理，若M₂在k步內接受 ω， 說明 ω 屬於S的補，則當i=k時，M會拒絕 ω 並停機。於是M就判定了語言S。

根據上述定理直接可得下述引理：

定理：HALTING 的補語言是圖靈不可識別的。

證明：很顯然 HALTING 是圖靈可識別語言，若它的補語言也是圖靈可識別的， 則根據上述定理知 HALTING 是圖靈可判定的，這和停機問題中證明的結論矛盾。